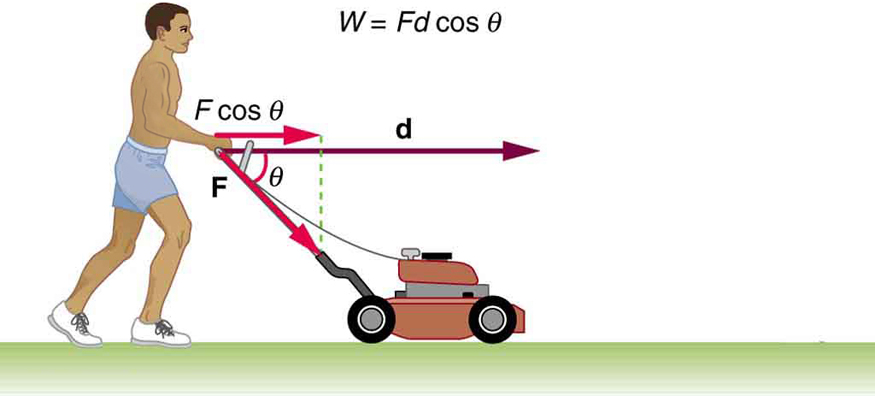The study of motion in our physical world involves a variety of quantities such as distance, displacement, speed, velocity, acceleration, force, mass, momentum, energy, work, power, etc. These quantities behave and or interact with each other in precise and predictable ways, including in relation to the structure of our bodies. For example the skeletal muscles and joints in our bodies are a complicated system of levers which allow us to move. The purpose of this module is to develop your understanding of aspects of some of these fundamental ideas, and how they tie in with the movement of the human body.Image: http://philschatz.com/physics-book/resources/Figure_08_02_04a.jpg
There are some superficial differences in the systems of notation used to represent vectors. In this module we will represent a vector quantity by placing a bar (or arrow) over the symbol (e.g., velocity is denoted by ῡ for velocity). In order to distinguish vectors from scalar, a symbol without a bar or arrow over it denotes a scalar quantity (e.g., the symbol υ without the bar denotes speed).
Example
A speed of 60 km/hr may be denoted: υ = 60km/hr
A velocity of 60 km/hr in a direction that is 20 degrees clockwise from north may be denoted: ῡ = 60 km/hr 20 degrees clockwise from north.
Vectors are represented in diagrams as line segments with an arrow head. An arrow has both a magnitude (how long it is) and a direction (the direction in which it points). The starting point of a vector is known as the tail and the end point is known as the tip or head.
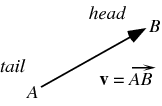
Image: mathworld.wolfram.com/images/eps-gif/Vector_1000.gif
When doing any mathematical operation (e.g., addition, subtraction, on a vector quantity you have to consider both magnitude and direction. This makes dealing with vector quantities a little more complicated than scalars. In summary:
- Scalars are added (or subtracted) arithmetically. For example, suppose you travelled 6km in your car along a straight road to a supermarket and when you finished shopping you then travel a distance of 2.2km back the way you came and stopped to have a cup of coffee. This scenario suggests that you have travelled a distance of:
6 km + 2.2 km = 8.2 km.
- Vector quantities are added geometrically (to take into account their direction). In the straight-line example above, “2.2km back the way you came” is represented as a negative direction. So the resultant displacement is 6km – 2.2km = 3.8km away from the start.
Note that the resultant is the vector sum of two or more vectors. That is, it is the result of adding two or more vectors together.
In order to draw a vector accurately we must specify a scale and include a reference direction in the diagram. A scale allows us to translate the length of the arrow into the vector's magnitude. For instance, if one chose a scale of 1 cm = 2 N (where N is the symbol for newton which is the unit for force), a force of 20 N towards the east, would be represented as an arrow 10 cm long. A reference direction may be a line representing a horizontal surface or the points of a compass.
Image: cnx.org/resources/3dbc4a7556e81eec8cf472866318c8ad/PG11C1_010.png
Example 1
A tennis ball is rolled towards a wall which is 10 m away to the right. If after striking the wall the ball rolls a further 2.5 m along the ground to the left, calculate the ball's resultant displacement. Note that a resultant vector is the vector sum of two (or more) vectors. In other words it is the result of adding two or more vectors together.
Answer
Draw a diagram to scale to represent the situation.
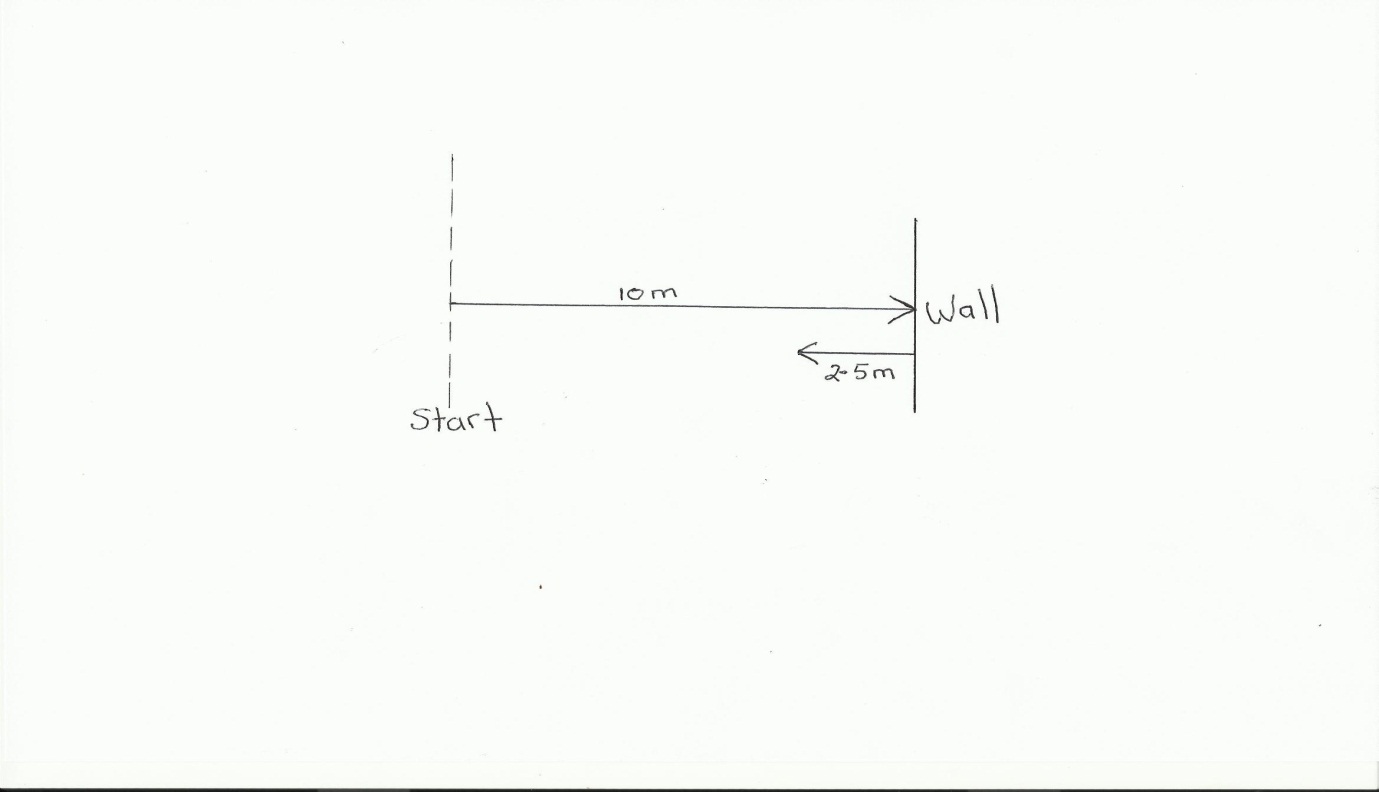
We know that the resultant displacement of the ball (
) is equal to the sum of the ball's separate displacements (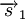 
and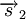 
):
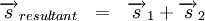
Since the motion of the ball is in a straight line (i.e. the ball moves left and right), we can use the method of algebraic addition just explained.
First we choose a positive direction. Let's make to the right the positive direction. This means that to the left becomes the negative direction.
With right positive:
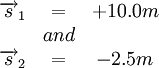
Next we simply add the two displacements to give the resultant:
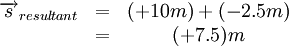
Finally, in this case right means positive so:
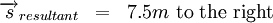
The following videos deal with the addition of two vectors that are not opposite in direction to each other in direction (as was the case in the example above). The first video explains two methods that can be used to add vectors. The second video works through an example of the addition of three vectors.
(Note that the vector equation written at the top of the blackboard in the second video describes the resultant vector (in this case the vector is velocity) as the sum of three vectors, with each vector represented by its magnitude (e.g., 6 m/s) and its direction (e.g., E30°N)).
Example 2The following worked example was sourced and adapted from the following website:http://cnx.org/content/col10322/1.175
Find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0º north of east. Then, she walks 23.0 m heading 15.0º north of east. Finally, she turns and walks 32.0 m in a direction 68.0° south of east. Each of the three displacement vectors have been labelled A, B and C respectively and are represented in the diagrams below. Note that the three vectors have been drawn on three separate axes but it would be just as appropriate to represent all three on the one set of axes.
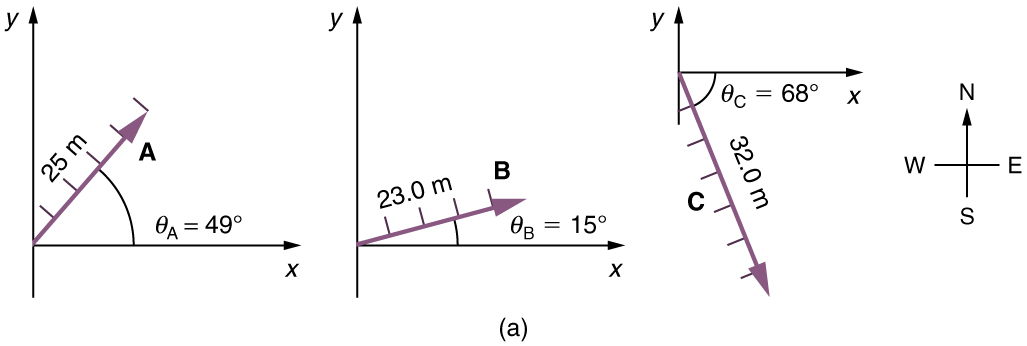
Image://cnx.org/resources/5d8d6294b8ed018811ba255dea7d749a/Figure_03_02_08.jpg
Answer Represent each displacement vector graphically with an arrow, labelling the first A, the second B, and the third C, making the lengths proportional to the distance and the directions as specified relative to an east-west line. The head-to-tail method outlined above will give a way to determine the magnitude and direction of the resultant displacement, denoted R.
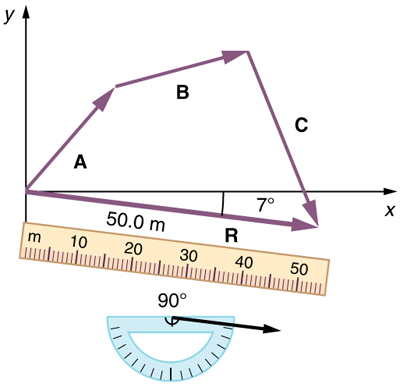
Image: http://cnx.org/content/m42127/latest/Figure_03_02_11a.jpgThe total displacement R has a magnitude of 50.0 m and is in the direction 7.0º south of east. By using its magnitude and direction, this vector can be expressed as R = 50.0 m and θ=7.0º south of east.
Example 3
Tension in cord = gravity force (N) = hanging mass (kg) × 9.8
Look at the figure of Hamilton-Russell traction below. Note that a cord attached to the knee, passes over 3 fixed pulleys and one moveable pulley, which is attached to the foot. A hanging mass of 4.25kg puts tension on the cord that supports the leg. Note that the pulleys change the direction of the cord so that the cord exerts a force on the leg at three places.
That is, there are three forces of equal magnitude (labelled F1, F2 and F3 in the figure) acting on the leg due to the cord.
The traction force on the leg is the resulting force from the vector sum of 3 forces (the pull of the cord at three places on the leg). Perhaps surprisingly, the traction force is parallel to femur but not to any section of the cord.
The magnitude of each force is 41.65N (=4.25kg × 9.8m/s) while the direction of each force is as shown by the direction of the force arrows. The magnitude of the traction force is greater than weight of hanging mass (due to the moveable pulley, a mechanical advantage is gained).
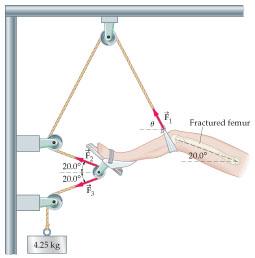
Draw (using a scale of 1cm = 10N) the vector that represents the tension (41.65 N) in the cord attached to the knee (F1) due to the 4.25 kg mass (it will be 4.17cm long).
Make sure that your vector is parallel to the arrow that represents force F1 in the diagram.
Add the other 2 force vectors (by placing their tail at the tip of the previous force vector).
Draw in the resultant vector and measure its length in cm and convert the length to newtons. (Note all 3 tension force vectors are the same magnitude and so the same length).
Describe the direction of the resulting traction vector in relation to the femur.
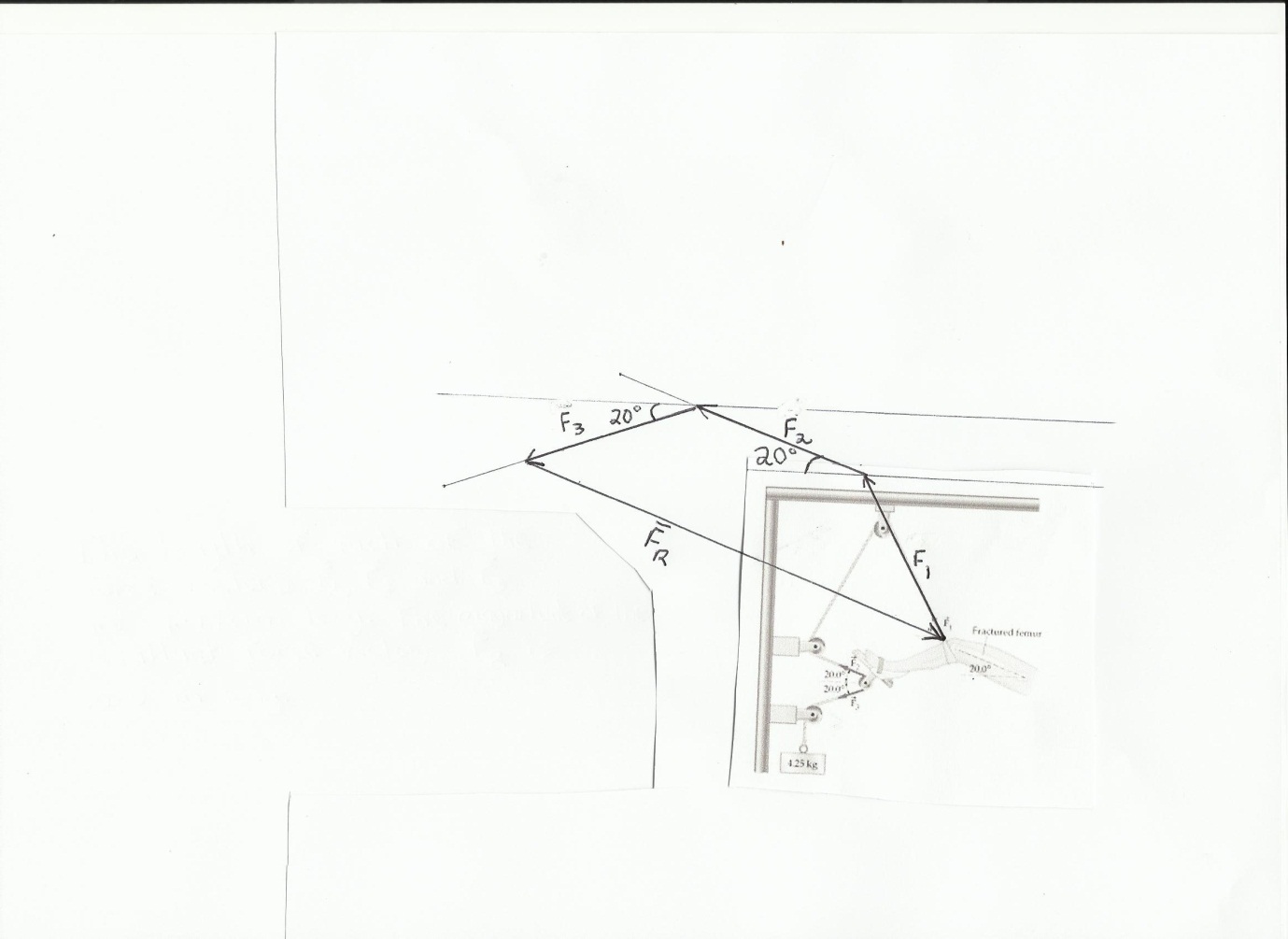
(ANS: magnitude is 10.5cm = 105N, direction is parallel to the femur)
Example 4
Many body movements require several muscles to contract simultaneously (the prime mover & synergists). The individual muscle tensions add like vectors to give the resultant force. If one muscle is damaged, the resultant magnitude & direction of action of the others will be compromised.
VM + VL + VI + RF = 2 + 4.5 + 3.5 + 4.3 = 13.8cm in the direction of
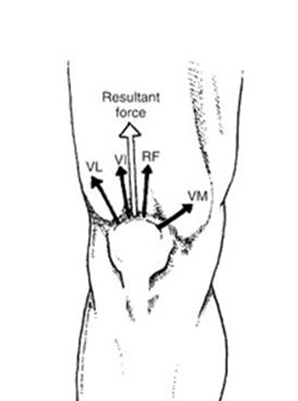
While our worked examples so far have involved finding the resultant vector graphically (by drawing them to scale), it is worthwhile introducing you to an algebraic approach that is appropriate to use when two vectors are at right angles to each other. You may notice in the following example that we have applied Pythagoras Theorem to calculate the resultant vector.
Example 5
Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement algebraically.
Answer
This problem asks to determine the result of adding two displacement vectors that are at right angles to each other. The result (or resultant) of walking 11 km north and 11 km east is a vector directed northeast as shown in the diagram to the right. Since the northward displacement and the eastward displacement are at right angles to each other, Pythagoras theorem can be used to determine the resultant (i.e., the hypotenuse of the right triangle).
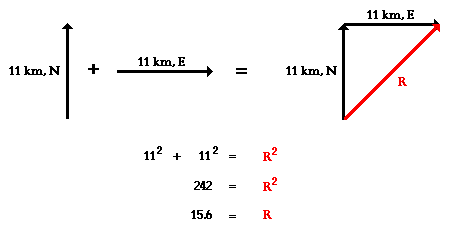
Image :www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Addition
Therefore the resultant displacement is 15.6 km in the direction North-East. You may also wish to find the resultant displacement by drawing the vectors to scale as was the previous method used in worked examples 1-4 and compare your answers.
1. Two vectors of the same magnitude are added; one pointing east, one west. The magnitude of the resultant vector is:
A 0
B 1
C 2
D 3
2. Which of the following is not a vector quantity?
A velocity
B Force
C time
D acceleration
3. A boat moves 10 km due west, 5 km due north, and then 10 km due east. The displacement of the boat from its initial position is:
A 5 km, North
B 10 km, East
C 5 km, South
D 0 km
4. You walk 31 m south and 31 m west. Your displacement is approximately:
A 22 m South west
B 44 m South west
C 44 M North west
D 62 m South west
5. Two football players hit a blocking sled. One hits it with a force of 350 N, East, and the other hits it with a force of 270 N, South. The resulting force is:
A 442 N, in approximately a south-easterly direction
B 620 N, South-East
C 80 N, South-East
D 442 N, South-East
6. A vector has both magnitude and __________.
A mass
B time
C direction
D none of the above
7. Graphical representation of vectors involves ______.
A drawing arrows
B units of measure
C direction but not magnitude
D none of the above
Click here to check your answers
