Please watch the following youtube video which explains the special classification of 3 dimensional solids.
Now watch the following video from Kahn Academy
The following exercise contains some basic 2D and 3D shapes and some of their properties.
Click here to access to the exercise.
The quick quiz at the bottom of this web page provides some feedback.
Quadrilaterals
A polygon is a plane figure with at least three straight sides and angles (See Geometry BI2). A quadrilateral is a polygon with four sides.
Here are two examples of polygons.
|
Convex quadrilateral |
Concave quadrilateral |
|---|---|
|
|
|
The above quadrilaterals are irregular, as all of the four sides are not the same length.
Quadrilaterals with four sides of the same length are regular quadrilaterals or shapes.
For example: A square is a regular quadrilateral.
Which of the following geometric shapes is also a regular quadrilateral?
|
Kite |
Rhombus |
Rectangle |
|---|---|---|
|
|
|
|
Click here to check your answer
Diagonals
The lines connecting non-adjacent corners or vertices of a polygon are diagonals.
Go to the GeoSET webpage (Oklahoma State University) to learn more about the diagonal properties of various quadrilaterals.
Please Note: that it is stated that a kite does not have perpendicular bisecting diagonals. Although the kite does have perpendicular diagonals forming four right angles where they meet, only one of the diagonals bisects the other (divides into two equal parts).
How many different quadrilaterals can you make by joining the dots on the circle (click on link below from NRICH enriching mathematics)?
Click on ‘Getting Started’ on the left hand side of the web page to print a copy of the circle.
For further ideas, click on ‘Solution’.
The four angles of a quadrilateral equal 360°. This is easy to see in a squares and rectangles, which have four right angles or square corners each measuring 90° (4 x 90° = 360°)
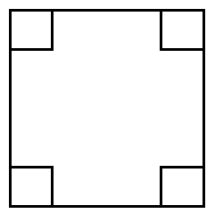
But what about other quadrilaterals, such as irregular ones?
Do their four angles total 360°?
Here is a way of finding out:
Draw various quadrilaterals, tear off the four corners and fit them back together as in the illustration below. The four corners (angles) with fit together to make a full revolution of 360°.
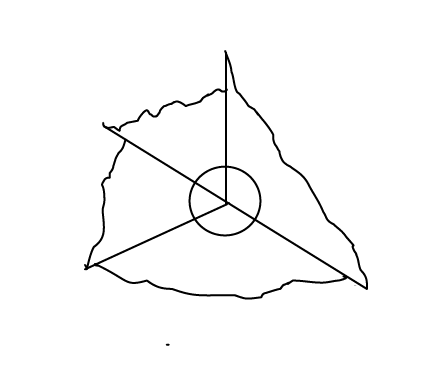
Here the corners of a kite have torn off and the corners have been put together. They equal 360° and therefore a kite is an irregular quadrilateral.
Use the same strategy of tearing off corners to discover how many degrees are in a triangle, making sure you try all three types of triangles viewed in Learning Object 1A: Common 2D and 3D shapes.
Extend this to other regular and irregular polygons such as …
|
Polygon |
Number of Sides |
Sum of Interior Angles |
|---|---|---|
|
triangle |
3 |
180° |
|
quadrilateral |
4 |
360° |
|
pentagon |
5 |
540° |
|
hexagon |
6 |
720° |
|
heptagon |
7 |
900° |
|
octagon |
8 |
1080° |
|
decagon |
10 |
1440° |
|
dodecagon |
12 |
1800° |
Area is the two-dimensional space within a region. Shapes with different dimensions or perimeters may have the same area.
A parallelogram is four-sided plane figure with opposite sides parallel.
Here are some quadrilaterals (four sided polygons).
All four are parallelograms because opposite sides are parallel.
square | rectangle | rhombus | parallelogram |
|---|
Finding the area of a rectangle by multiplying the length and width (breadth) is usually the first formal method to which students are exposed.
The area of the blue rectangle in the diagram below is 12 units2, or 12 square units (4 x 3).
The area of the purple square is 16 units2, or 16 square units (4 x 4).
The area of the yellow rectangle is also 16 units2, or 16 square units (2 x 8).
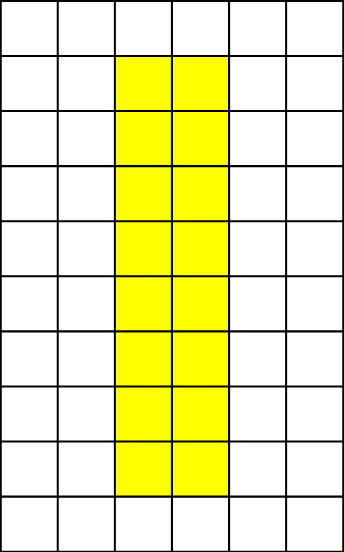
Multiplying the length and width give the same result as counting squares.
The area of this rectangle is 46m2 or 46 square metres (4 x 11.5). 
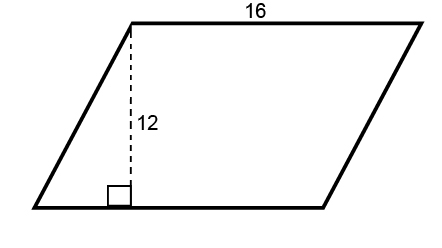
To find the area of a parallelogram, it is important to recognise that the height must be at right angles with the base (the perpendicular height).
Imagine sliding the triangular segment on the left towards the right and fitting it into the space on the right of the parallelogram. The diagram below shows how the area of a parallelogram is the same as the area of the rectangle into which it has been transformed:
The shape below would be transformed into a 16 x 12 rectangle. This is why the perpendicular height must be used.
The area of this parallelogram is calculated by multiplying 16 by 12.
16 x 12 = 192 units2
Watch the following video to see this demonstrated. The video shows how knowing how to calculate the area of a rectangle can allow us to calculate the area of triangles and parallelograms:
Three dimensional shapes have as the name suggests have 3 dimensions: length, width and height.
Some common 3D shapes are shown below:
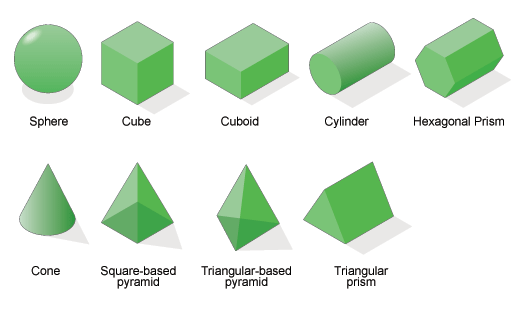
http://www.bbc.co.uk/bitesize/ks3/maths/images/solids.gif
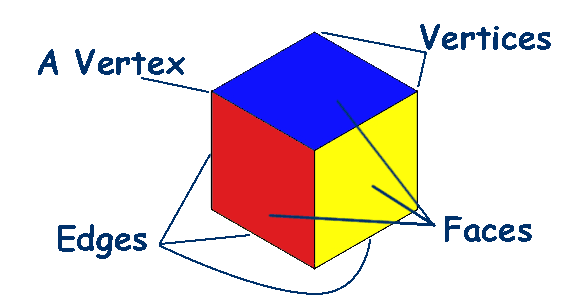
3 dimensional shapes such as the cube below have faces, edges and vertices and these shapes are called Polyhedra (polyhedron singular).
The 3 D shapes shown in the next illustration are called Platonic shapes. Among other interesting properties the faces of Platonic shapes are all identical regular polygons. There are just 5 platonic shapes.
Tetrahedron Cube Octahedron Dodecahedron Icosahedron
http://wordpress.mrreid.org/wp-content/uploads/2011/10/platonic-solids.png
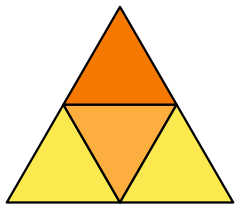
Imagine what these and other 3 D shapes would look like if they were folded out into their 2 dimensional nets. For example the net of the tetrahedron is shown below. Imagine folding the 3 outside triangles up to meet at a point.
Here is an interactive link from Khan academy that gives you the opportunity to look at different 3D shapes and predict what their nets could look like.
All Khan Academy content is available for free at www.khanacademy.org
The following diagrams show you two different nets of a cube. There are actually 11 different cube nets that can be drawn.
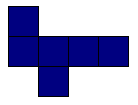
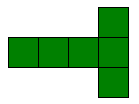
1. Draw two more nets which could be folded to construct a cube.
2. Draw a net for a rectangular prism.
3. Consider the properties of a cylinder and draw a net for it.
Once you have drawn the nets above, check your cylinder net and investigate other nets using this link from Illuminations - Resources for Teaching Math:
1. Select ‘nets’ in the tool bar under the word ‘Instructions’
2. Select the shape ‘cylinder’. The dimensions should appear for you. Select cm not inches.
3. Click on ‘add’ and you will see the three 2D pieces to make up a cylinder – two circles and a rectangle.
4. Clicking on the trashcan will erase the image.
5. Investigate other 2D nets for various 3D shapes.
A circle is a plane (2D) figure or shape. Its boundary (circumference) is always a fixed distance (radius) from the centre. The diameter of a circle is twice the length of the radius.
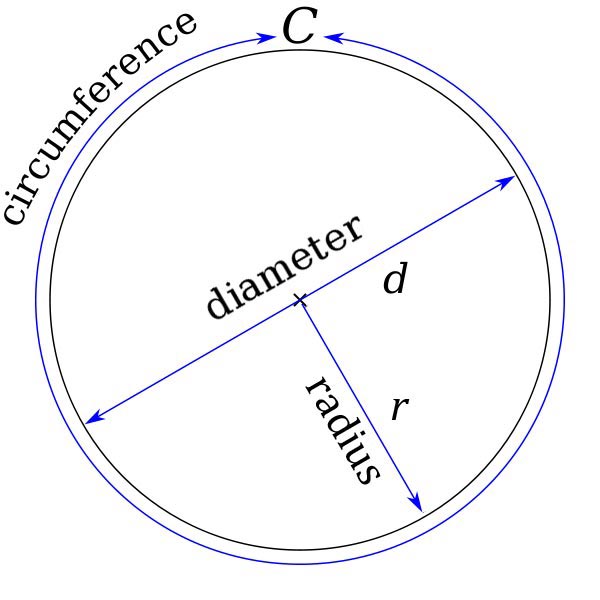
http://upload.wikimedia.org/wikipedia/commons/3/36/Pi_eq_C_over_d.svg
Go to the following link from the Maths is Fun website to find out more about a circle:
From the above link, you would have discovered that when you divide the circumference by the diameter you get 3.14159…which is called pi(π).
Because the radius is half the length of the diameter, it makes sense that the circumference length is 2 x Radius x π, usually written as 2 π R.
Exercise 1:
Click on the following link to see a visual simulation to help you remember that the circumference is three and a bit (3.14159…) times the length of the diameter, or six and a bit times (2 x 3.14159…) the length of the radius.
from Illuminations Resources for Teaching Maths
Click on the blue d for diameter, then on the video camera, and watch the circumference of the circle.
Click on the red r for diameter, then on the video camera, and watch the circumference of the circle.
Exercise 2:
Hopefully you will find the following video quite fascinating, as the graphics help demonstrate how a circle can be transformed into a rectangle, demonstrating where the formula for the area of a circle, π R2, comes from.
You are making a cylinder, and you have the two circular ends, each with a diameter of 400mm.
You need to construct a body to fit the ends of the cylinder.
The following pentagon has been divided into triangles by drawing the diagonals from one vertex:
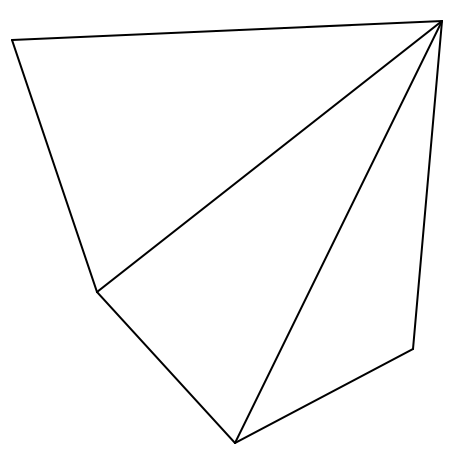
Considering that the sum of the interior angles in a triangle is 180°, we can workout that the sum of angles in a pentagon is 540° (3 x 180°).
Using this ‘triangles’ strategy, use similar diagrams to show how to calculate the number of angles in
Notice that the number of triangles created by drawing all the diagonals is 2 fewer than the number of sides in the polygon i.e. (n – 2). Each of the triangles has an angle sum of 180° so for any polygon you can use an equation to calculate the sum of the interior angles of any polygon:
Sum of interior angles = (number of sides – 2) x 180°
This relationship between the number of sides and the sum of the interior angles can be expressed as follows:
s = (n - 2)180° where:
s = the sum of the interior angles.
n = the number of sides of the polygon.
This can be applied to a polygon with any number of sides.
Example
To calculate the sum of the angles on a 20 sided polygon:
s = (20 – 2) x 180°
s = 18 x 180°
s = 3240°
Geometry is important because it links many areas of mathematics including algebra, measurement, and data.
Practice Task
a) Use the above information on the sum of interior angles to find the missing angle (x):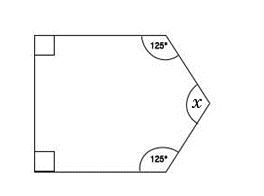
b) What is the size of each angle in a regular 14 sided polygon?
This module serves as an introduction and depending on your prior knowledge, a revision or consolidation of the basic properties of shapes.
These geometric properties determine what makes shapes alike and different in mathematically important ways.
In this Big Idea you should now understand
These skills will assist in the development of deductive reasoning skills (Geometry BI2) to form geometrical conclusions.
Please proceed to Geometry - Big Idea 2
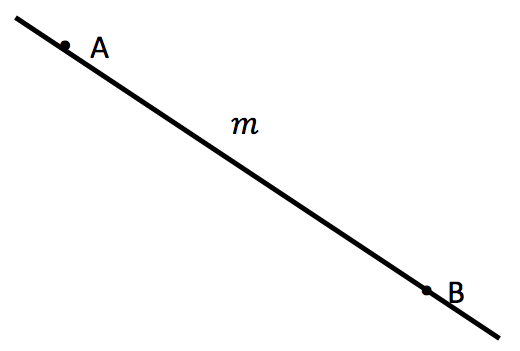
A line extends in two directions indefinitely, unless we specify the end points.
Points can be plotted on a line.
The segment of line between A and B can be referred to as the line AB. It can also be referred to by a lower case letter, in this example m.
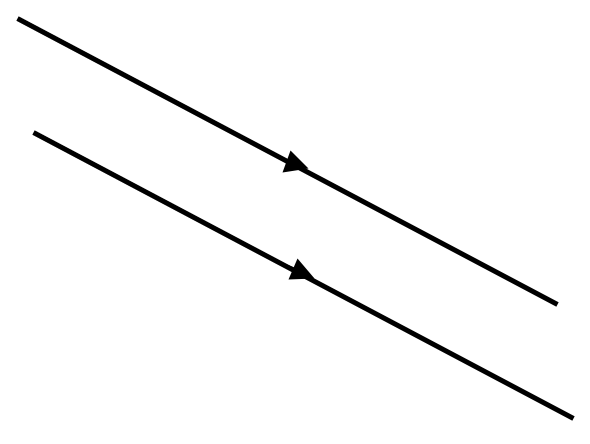
Lines in the same plane which never meet are parallel. They are always the same distance apart.
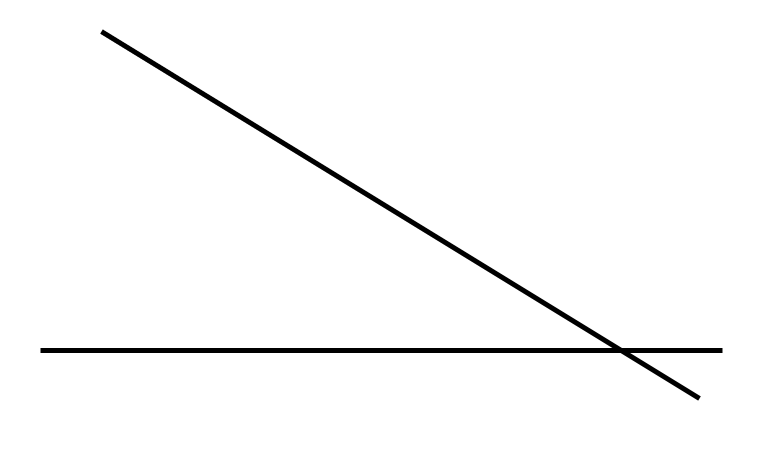
If the two lines are not parallel, they will eventually meet or intersect. These two lines intersect.
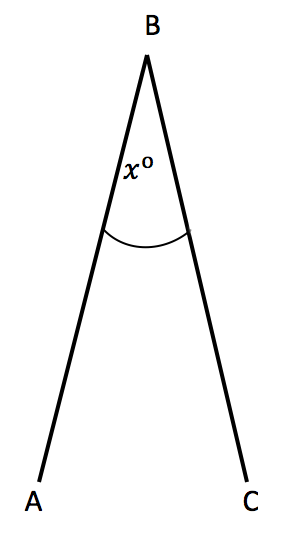These two lines meet at the point B, and form the angle ABC (∠ ABC).
The amount of turn around the point of intersection from one line to another is referred to as an angle. The arc shows the amount of turn. It is usually drawn close to the point of intersection but could be drawn anywhere between the two rays without making any difference to the size of the angle.
Angles are measured in degrees (°).
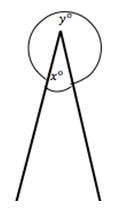Unless specified, angles usually refer to the smaller angles, such as ∠ ABC above.
The angle y in the diagram on the left is a reflex angle.
One full revolution, such as is formed by adding x° and y° in the diagram on the left, is 360°.
Angles can be classified or named according to their size:
|
Right Angle 90°
|
Acute Angle Less than 90° (<90°)
|
Obtuse Angle Greater than 90° (>90°) |
Straight Line Angle 180°
|
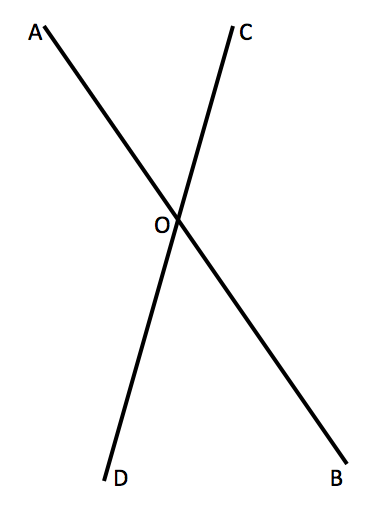When two lines intersect, four angles are formed at the intersection point. The total measure or sum of these angles is 360o (one full revolution).
The four angles are made up of two pairs of vertically opposite angles. In the diagram to the left, the two pairs of vertically opposite angles are:
∠ AOC and ∠ DOB
∠ AOD and ∠ COB
Vertically opposite angles are always congruent, that is, equal.
Click on the following link to discover how knowledge of vertically opposite angles can be used.
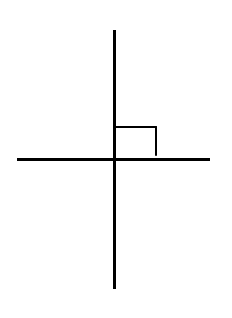
When two lines intersect at right angles, they are said to be perpendicular to each other.
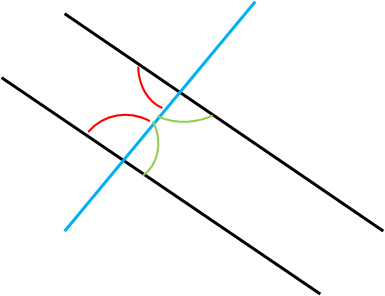
A transversal is a line which crosses at least two other lines. When a pair of parallel lines is crossed or traversed by a line, as in the diagram below, the corresponding angles formed are always congruent (equal). The corresponding angles are the ones in the matching corners, as indicated by the arcs.
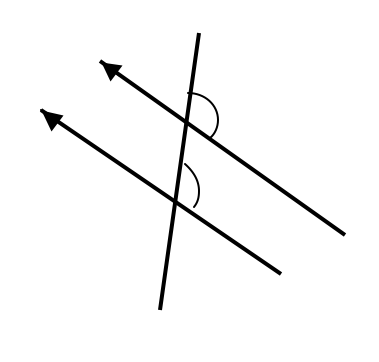
In the diagram below the two parallel lines are traversed by the blue line.
The pairs of angles on the same side of the transversal but inside the two lines are called cointerior angles. They can also be referred to as consecutive interior angles.
In the diagram below, there are two pairs of cointerior angles, one pair shown in red and the other pair shown in green.
If the two lines are parallel, the sum of the cointerior angles is always 180°.
Learning Activity 2
Estimating Angles
Go to the link below and use the following information to estimate angle sizes.
There are three levels of progression, but if you use the above angles as a benchmark, levels two and three should be no harder than level one.
The following link provides the definition of a rectangle as a “4-sided flat shape with straight sides where all interior angles are right angles (90°)”. In addition, “opposite sides are parallel and of equal length.”
Before you click on the web page to find the answer, use this information about the properties of a rectangle to deduce (reason) whether or not a square is a rectangle.
Work through the following page from Maths is Fun
Were you able to move a corner of the rectangle to turn it into a square? Did the definition of rectangle still apply?
Now that you know that a square is a special type of rectangle, you can complete the following web activity from NRICH enriching mathematics.
You can click on ‘solution’ on the left hand side once you have had a go.
Now you can use what you know about complete revolutions, straight angles and right angles to answer the following question:
What is the size of angle COB?
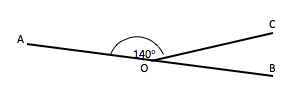
Check: Did the two angles add up to 180°?
Click here to check your answer.
Now you can use what you know about complete revolutions, straight angles and right angles to answer the following question:
What is the size of the fourth angle?
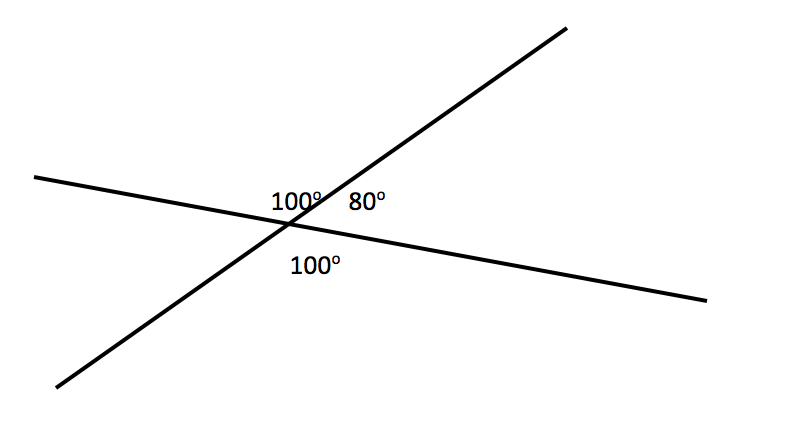
Check: Did the four angles add up to 360o? Are the vertically opposite angles equal?
Click here to check your answer
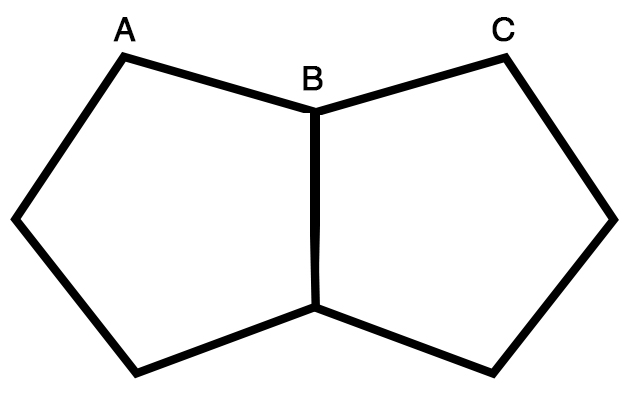
What is the size of the angle ABC?
Clue: The two pentagons are regular polygons (see Geometry module 1) with all sides of the same length. If all sides are the same length, then all angles are the same.
In Geometry module 1 you saw that
s = (n - 2)180° where:
s = the sum of the interior angles.
n = the number of sides of the polygon
Click here to check your answer
What is the measure of the angles marked x° in the pentagon below?
(Diagram is not to scale)
There is more than one strategy to solve this.
These clues may give you some ideas:
In Geometry module 1 you saw that
s = (n - 2)180° where:
s = the sum of the interior angles.
n = the number of sides of the polygon
The pentagon shown below is symmetrical (see Geometry BI3). This means that if it is folded vertically along a line joining the midpoint of AB with D the two parts will overlap exactly. This may help you visualise how the pentagon can be partitioned into two quadrilaterals. Visualisation is an important feature of the development of spatial sense or intuition about shapes and the relationships among them.
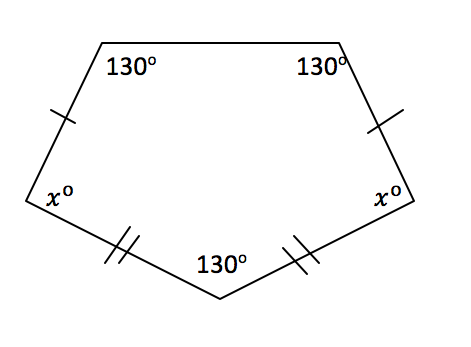
Click here to check your answer
The following diagrams show the diagonals of three rectangles, one being a square.
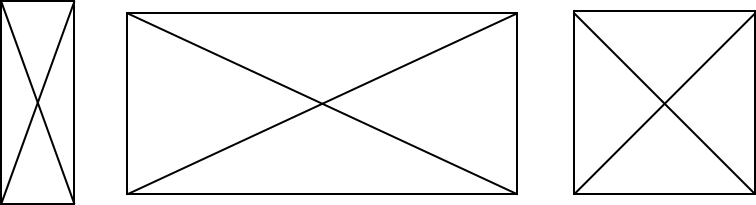
Look closely at the features of the three diagrams. What properties of diagonals do you think will guarantee that you will have the particular rectangle that is a square?
Click here to check your answer
Transformations are processes that happen to shapes.
The main types of transformations are:
The videos in the Learning Activities 1 - 4 provide thorough explanations of these different ways of transforming shapes in a plane.
You will notice that when a shape has been transformed in these ways the original shape and the resulting shape are still congruent, that is, the perimeters, side lengths, angles, areas and shapes remain the same. For example, an ‘L’ shape remains an ‘L’ shape, but it may be upside down.
When the shape is transformed its congruent shape ends up in a different position on the plane. The different position means that they are not the same shape. Position must be taken into account. You will see this demonstrated in the videos through use of coordinates. The use of coordinates assists us to describe the location of shapes in a plane. Using coordinates can help us to understand and visualise the transformation of shapes on a plane.
You can practice the manipulation of shapes through a simple program such as Microsoft Word – Shapes, or dynamic imagery software such as GeoGebra, which is free.
In this video you will see how every point in a shape moves the same distance and in the same direction when the shape undergoes a translation.
In the following video, notice how the point of rotation must be identified.
Watch the following video which demonstrates how a coordinate system on a grid is used to describe the movement and position of transformed shapes.
Reflections are mirror images of each other.
The mirror line or line of reflection is referred to as the axis of symmetry.
Line symmetry occurs when the shape of an object on one side of a line (or axis of symmetry) can be matched to the shape on the other side of the line. Each reflected point is the same distance away from the line as the other side.
Go to the following link from Maths is Fun and complete the quiz at the end. You can redo any questions you got wrong. If you are still not sure, cutting out a paper version of the shape and folding will assist you to identify the lines of symmetry.
You would have noticed tessellations all around you, especially on roofs, walls, paths and floors. They are patterns made by repeatedly fitting together the same shapes or tiles to cover an area. There must be no gaps or overlap, so not all 2D shapes will tessellate. The pattern can be continued indefinitely in any direction.
To decide whether or not a shape will tessellate, we need to consider the properties of the shape. The shapes may need to be manipulated or transformed using flipping, sliding or rotating.
There are only three regular polygons that tessellate. For there to be no gaps or overlaps in the tessellation, the sum of the angles meeting at each vertex (corner) must be 360°. One of these regular polygons is a square, because the sum of the four right angles is 360°. Think of what the other two regular polygons that tessellate may be.
Of course, many irregular polygons may also tessellate.
Photo: Tesselated Pavement at Eagle Hawk Neck, Tasmania
http://strangestplaceonearth.wikidot.com/eaglehawk-neck-tasmania
The following activity from NRICH enriching mathematics demonstrates tessellations made using the three regular polygons that tessellate, and also demonstrates tessellations made with two other shapes. You can experiment with making your own tessellations. While you do this, you will notice the angles of the different polygons and discover why not all polygons tessellate.
A tangram puzzle consists of seven shapes ( a square, a parallelogram, two big right angle triangles, a medium right angle triangle and two small right angle triangles). The shapes fit together in different ways to form polygons such as large squares, rectangles and triangles. Tangrams are often transformed into figures that resemble such things as animals.
Manipulation of tangram pieces provides a physical way to understand and develop geometric ideas.
Click on the following link from Illuminations- resources for Teaching Math and complete the tangram challenges in lessons one and two using the virtual tangram tool.
Click on the link below to solve the paving brick problem from NRICH enriching mathematics.
The solution can be found on the top left hand side of the web page.
A solution to the paving brick problem (click on top left hand side of the NRICH page) is offered using the Fibonacci sequence, which you may wish to further investigate to extend your knowledge. There is much information on the internet about this sequence, where each number is the sum of the two preceding numbers. Any two consecutive numbers in this sequence approximate the Golden Ratio 1:1.161…. You will find it fascinating to see how the Fibonacci sequence occurs in nature and has been used in design for many centuries.
Here are some interesting links about the Fibonacci sequence:
from Creative Bloq
Geometry Big Ideas 1 and 2 included content on the properties of shapes.
The Geometry module aims to demonstrate how shapes can be moved in a plane or space by flipping (reflecting), sliding (translating) or turning (rotating). The ability to reflect on and visualise the transformation and manipulation of shapes is a useful life skill can be referred to as dynamic imagery.
The application and integration of understandings of transformation, manipulation and visualisation to investigate shape and space can be referred to as geometric reasoning. This way of thinking is utilised by architects, engineers, builders, designers and artists. Everyone can develop these skills with experience and practice.
You are now ready to take the quiz for Geometry.
Good Luck!
Click here to take the quiz
