We encounter ideas related to fractions, decimals, ratios and percents on a daily basis. Confident and flexible understanding of these ideas are key to everyday estimation and mental calculation in contexts as diverse as shopping and budgeting, diluting mixtures, understanding scales on maps, interpreting probabilities and odds, and converting among metric units.
Not only is understanding these ideas essential to being numerate they are also foundational to more sophisticated mathematical ideas. If you understand fraction, decimals, ratios and percents you have the basis for understanding topics such as similarity, trigonometry, coordinate geometry, and fancy algebra
We use fractions every day, quite often to describe parts of a whole such as half an hour, third quarter of the netball game, one quarter of a cup of sugar or the bath being two thirds full.
The part/whole meaning of fractions, expressed as 
, is used when a part is being compared to the whole.
The numeral above the dividing line is referred to as the numerator, the dividing line is known as the vinculum, and the numeral below the dividing line is known as the denominator.
In the case of the fraction three fifths
(
)
the numerator is three (3) and the denominator is five (5).
The numerator signifies to the number of pieces of the whole lot, and the denominator signifies the number of pieces of equal size into which the whole is divided.
The part/whole meaning of fractions can be demonstrated in the following everyday examples:
Example 1
If $5.00 is shared between two people, and person A receives $3.00 and person B receives $2.00, person A’s share is three fifths () of the whole ($5.00) and person B’s share is two fifths (
) of the whole ($5.00).
Example 2
A class of sixty (60) students is comprised of thirty six (36) females and twenty four (24) males. We can see that thirty six out of sixty (
) students are females and twenty four out of sixty (
) are males are males. The two fractions can be read as thirty six sixtieths and twenty four sixtieths.
This part-whole concept can be represented in a diagram:
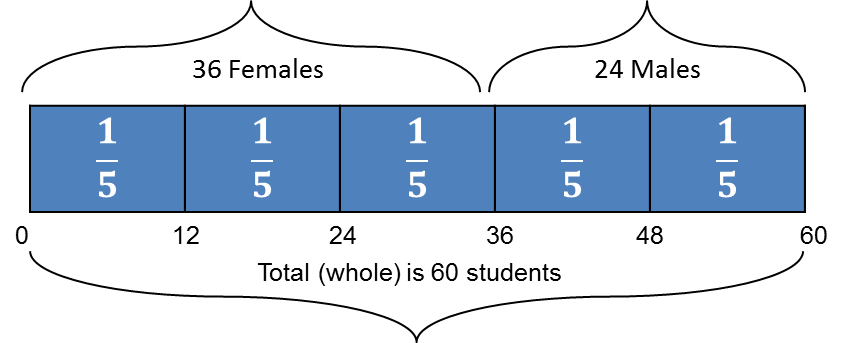
A common factor of both the numbers, thirty six (36) and twenty four (24) is twelve (12). Twelve (12) is one fifth (
) of the total sixty (60), as five times twelve is sixty (5 x 12 = 60). Five (5) is the lowest common denominator for these given fractions.
As well as saying that thirty six out of sixty () students are females and twenty four out of sixty () are males, we can say that three out of five () students are females and two out of five () students are males.
The fractions andare read as three fifths and two fifths.
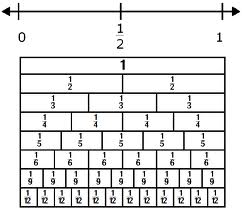
The fraction wall (link below) demonstrates the partitioning of an area model for one whole (1), in this case the model being one long brick. The one long brick is divided into several equal parts or fractions, with no remainder. It demonstrates two important understandings;
1. The larger the number of parts the smaller each part
The first three settings at the top should be ‘mixed’, ‘fraction’ and ‘off’.
, the numerator 1 showing the number of parts, and the denominator 2 showing the number of equal parts into which the one whole is divided.
. The whole is divided into four equal parts, not two as in the previous bar. There are more parts, but the whole is the same, so each part or fraction must be smaller. In fact, you will notice that each green quarter is half the size of each yellow half. You will also notice that as the parts get smaller, the denominator gets bigger (more parts).
) is half the size of a quarter (
). Notice the relationship between halves, quarters and eighths. As the number of parts doubles the size of each part halves. (see FDRP BI3 – add link)2. Equivalent fractions
). As the two quarters are the same size as the one half, one half () and two quarters (
) are known as equivalent fractions.
. These three fractions are equivalent fractions; they all have the same value.
).
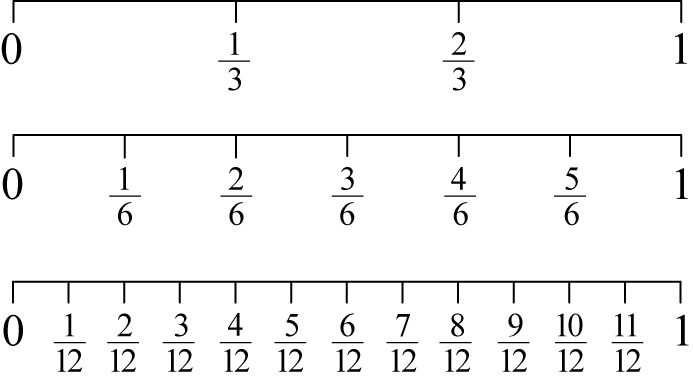
All numbers can be located on a number line. A number line can be used to compare and order fractions.
Think of the fractions wall as a number line (below).
The number line below represents eighths, that is, fractions with a denominator of eight. Each one (whole) has been divided into eight equal parts.
To reach the three eighths position for example, three steps to the right are taken, starting at zero. Each step has a length of one eighth.
We can see that the fractions on the same point on the number line are equivalent fractions.
That is:
=
=
=
=
The following video demonstrates how to plot fractions on a number line, considering the number of total parts into the one whole needs to be divided (denominator) and the number of those parts to be shown (numerator).
All Khan Academy content is available for free at www.khanacaemy.org
You can use the Battleship Number Line Game to practice and build your estimation and visualisation skills when placing fraction and decimal numbers on a number line.
When playing this game, try using more common fractions and equivalent fractions as a guide to placing fractions and decimals in the correct position.
For example:
on the number line it may be easier to visualise where the equivalent fractionwould lie.
on the number line, it is a little further to the right () thanor.
) greater than one tenth (one hundredth more).Number lines can assist with addition, subtraction, multiplication and division of fractions (also see Fractions as operators further down on this page). Each of the following examples is demonstrated on the number line below it:
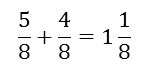
Start on then jump four more eighths to the right.
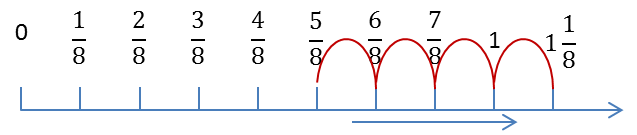
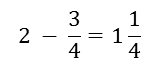
Start on 2 then jump three more quarters to the left.
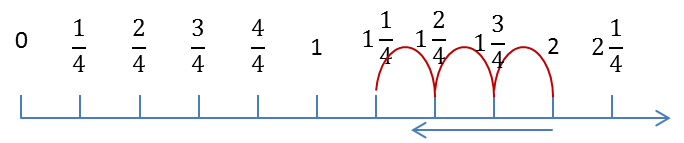
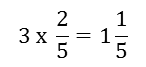
Start on 0 then jump a length of two fifths three times.
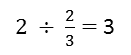
Another way of saying this is, “How many lots of two thirds are there in two?” Start on 0 and count how many jumps in lengths of two thirds are needed to get to 2.
The term improper fractions is used to describe fractions greater than one, such as 
(ten quarters). Representations of a fractions greater than one, with the numerator being greater than the denominator, is frequently used in algebra.
Improper fractions can also be written as mixed numbers. The diagram below shows how(ten quarters) can also be expressed as
(two and two quarters).
We can clearly see that or is equivalent to
The decimal notation for this is 2.5 (two point five).
Fractions are commonly used as measures.
To extend the idea of fractions as numbers, imagine that the following number line is a tape measure used to measure a length of ribbon. The arrow is pointing to two and a quarter metres (
m) of ribbon, which is expressed in decimal fraction notation as one point two five metres (2.25m).
Fractions are often used to measure time, for example:
A fraction acts as an operator when it is applied to a number, set or quantity to find a certain proportion of that number, set or quantity.
Example 1
Find three quarters of twenty four.
There are many ways of solving this. It would be straightforward to find one quarter of 24 (six) and multiply this by three to find three quarters, giving an answer of 18.
Example 2
The original cost of an oven ($1,200) is reduced by. What isof $1,200? What will the discounted price be?
One way to solve this is;
(x 1200) is the same as 1200 ÷ 5, which is 240.
Therefore the discounted price would be $1200 - $240 = $960.
Notice the word of, which is indicative of the operation of multiplication.
Notice also that multiplying by a number which is less than one (e.g.or) results in a smaller number.
Fractions can be used as a representation of division.
Example 1
A quotient such as 3 ÷ 4 can be represented by.
Numbers that can be expressed in this way
Asare known as rational numbers and can be derived from dividing the numerator by the denominator.
Example 2
Three people have to share two choc bars. How much does each person get?
Here is one way to visually represent this problem:
Each person receives one third of each bar, therefore two thirds (
) of a chocolate bar.
Two shared among three can be represented by the division 2 ÷ 3, which is the same as.
Conversely, the symbolcan be referred to as two divided by three.
The quotient of two divided by three is two thirds.
The following video shows how paper-folding strips of paper are used to solve division of whole numbers where the quotients are fractions.
Fractions can be interpreted as ratios.
Example 1
In the pictures below there are 5 puppies, 3 females and 2 males.
The ratio of males to females is 2:3 or
Ther ratio of females to males is 3:2 or
The ratio of males to all the puppies is 2:5 or
The ratio of females to all puppies is 3:5 or
When using or interpreting ratios, an important aspect is to be clear about is whether the comparison is Part-to-part or Part-to-whole.
Fractions are used more commonly to represent part:whole ratios.
Example 2: Part-to-part representation
Example 3: Part-to-whole representation
.
are picture cards.
1. Starting atwrite a sequence of eight numbers counting by:
a) One half
b) One quarter
c) One tenth
d) One twelfth
2. Find equivalent fractions for:
a)
c)
3. Show how you can calculate:
a)
b) ÷
c)
d)+ 
4. Place the following numbers on a number line:
a) 2 1 
b) 0.5 2.25 0.9 2 1.75 2.8 2.4 0.2 1.5 1
Click here (PDF 442.2 KB) to check your answers.
Solve the following problems where fractions are used as operators. There is more than one way to solve each of these problems and thinking about different strategies can be helpful.
of the floor tiles needed to be replaced. The total number of equal sized tiles on the floor was 60. How many tiles had to be replaced?of their marked price? of 45 or
of 40?is a larger fraction than, as they relate to different wholes).Click here (PDF 438.4 KB) to check your answers
Draw a visual model to show how six pizzas can be equally shared among eight people if:
Identify whether the following problems are Part-to-part or Part-to-whole representations and represent the answers using a ratio:
Timber Town has a population of 200 people, 40 of these being children.
a) What is the ratio of children to the town’s population?
b) What is the ratio of adults to the town’s population?
c) What fraction of the town’s population are children?
d) What fraction of the town’s population are adults?
On a school excursion, there is one adult supervisor for every group of six children.
a) What is the ratio of supervisors to children?
b) If there are 36 children, how many adult supervisors are required?
c) What fraction of the people on the excursion are supervisors?
Click here (PDF 448.4 KB) to check your answers
The purpose of this module was to identify how:
To demonstrate the following understandings:
a pizza is bigger thanof a pizza if both of these fractions are parts of the same pizza (ie the same whole). This would not be the case if we were talking aboutof a small pizza andof a large pizza.
http://syllabus.bos.nsw.edu.au/assets/mathematicsk10/images/s3na043.png
you can use the unit fractionand measure to show that it takes 5 of these to makeof the class went to the swimming pool during the holidays this means that 16 students in my class went to the pool. 
. Ratios can be part-part or part-whole. If we consider the ratioa part-part example could be “the ratio of people who own a dog (part) to those who do not own a dog (part)” whereas a part-whole example could be “the ratio of people who own a dog (part) to the people in your suburb (whole).
Does this make sense to you now?
Proceed to Big Idea 2 in the Relationships between Fraction, Decimals, Ratios and Percentages module
The word 'Decimal' comes from the Latin word decem meaning ten. The decimal system has 10 as its base and is sometimes called a base-10 system. This means that the decimal system is based on "bundles of ten" and using the digits 0,1,2,3,4,5,6,7,8,9 as represented in the diagrams below;
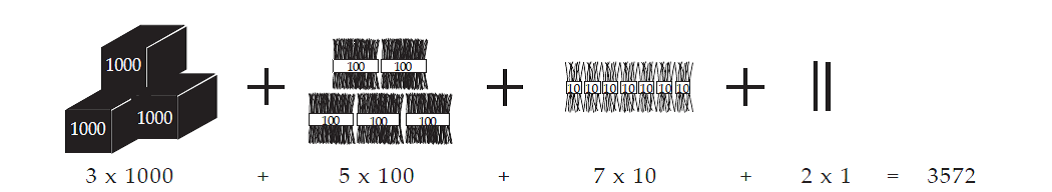
In the decimal system the decimal point separates the ones place from the tenths place. The system of decimal numbers is an extension of the system of whole numbers (see PV Module). Whole numbers are written as digits that correspond to the 'places' ones, ten, hundreds and so on. Positive numbers less than one can be written using the same notation with additional places to the right of the decimal point, such as tenths, hundredths, thousandths and so on.
x 24) than to use the decimal equivalent of one third (0.333333 x 24). The threes in this decimal go on indefinitely.Watch the following video about the classification of numbers
The video shows how fractions and decimals fit into our number system.
The system of decimal numbers is an extension of the whole number system. (See Place Value module, Big Idea 1, Learning Objects 1.1, 1.2 & 1.3)
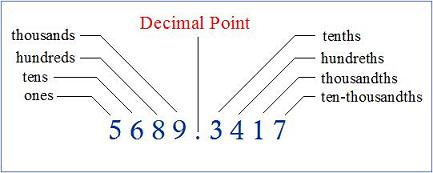
Decimal numbers contain a decimal point, which identifies where the ones place is located, that is, immediately to its left.
The decimal point also signifies the values of the digits to its right, being tenths, hundredths, thousandths and so on.
The position of a digit in a number determines its value.
In the above number…
The 3 is in the hundreds place, so the value of the 3 is 300 (3 x 100)
The 4 is in the tens place, so the value of the 4 is 40 (4 x 10)
The 5 is in the ones place, so its value is 5 (5 x 1)
The 1 is in the tenths place, so the value of the 1 is 1 tenth or 0.1 (1 x
)
The 2 is in the hundredths place, so it represents 2 hundredths or 0.02 (2 x 
)
The 5 is in the thousandths place, so it represents 5 thousandths or 0.005 (5 x 
)
The 8 is in the ten thousandths place, so it represents 8 ten thousandths or 0.0008 (8 x
)
Any number can be renamed in terms of its place value parts.
(See Place Value module, Big Idea 1, Learning Objects 1.1, 1.2 & 1.3)
Below are some examples of how a number, in this case 345.1258, can be written in expanded notation.
345.1258 = 3 hundreds + 4 tens + 5 ones + 1 tenth + 2 hundredths + 5 thousandths + 8 ten thousandths
or
345.1258 = 300 + 40 + 5 + 0.1 + 0.02 + 0.005 + 0.0008
or
345.1258 = 34 tens + 5 ones+ 1 tenth + 25 thousandths + 8 ten thousandths
As the video has shown, all whole numbers and fractions are rational numbers, which can be written as exact decimals.
Example
The fraction three quarterscan be written as a decimal. Three quartersis equivalent to seventy five one hundredths,
, and therefore can be written as the decimal zero point seven five (0.75).
The next module/big idea will demonstrate how this is equivalent to seventy five percent (75%).
Here are further examples:
| Rational Number | Expressed as a Fraction | Expressed as a Decimal |
|---|---|---|
|
three fifths |
|
0.6 |
|
nineteen |
|
19.0 |
|
five and two tenths |
|
5.2 |
|
two thirds |
|
|
|
one eighth |
|
0.125 |
An interesting example of an irrational number is Pi (Ï€). It cannot be expressed as a fraction a/b where a and b are whole numbers (see module 1).
The value of pi = Ï€ is 3.14159… This decimal value goes on forever. This decimal number goes on for ever with no repeating pattern.
The following link shows Pi to one million decimal places!
The YouTube video below is a fun and interesting way to think about the kind of number that Pi is.
1. Longer is larger
A common misunderstanding when comparing numbers originates from the separation of decimal numbers into two whole numbers; that is, the sets of numbers on each side of the decimal point are treated as whole numbers.
The following examples show how this misunderstanding can go unrecognised because sometimes it results in a 'fluke' correct answer:
| Which is smaller? | Incorrect reasoning | Correct reasoning | Correct answer |
|---|---|---|---|
| 5.17 or 5.6 | 5.6 is smaller, because 6 is less than 17 | 5.17 is smaller because it has one tenth while 5.6 has six tenths. The seven hundredths are not relevant as they are smaller than tenths | 5.6 |
| 6.42 or 6.801 | 6.42 is smaller, as 42 is less than 801 | 6.42 is smaller because it has four tenths while 6.801 has eight tenths | 6.42 |
| 14.5 or 14.50 | 14.5 is smaller as 5 is smaller than 50. | They are both have the same value because 5 tenths is the same as 50 hundredths | Both the same |
2.Shorter is larger
This is another common misunderstanding when comparing numbers. It occurs when the decimals are incorrectly seen as fraction denominators: the larger the denominator, the smaller the fraction.
The following examples show how this misunderstanding can go unrecognised, as sometimes it results in a 'fluke' correct answer:
| Which is smaller? | Incorrect reasoning | Correct reasoning | Correct answer |
|---|---|---|---|
| 7.12 or 7.6 | 7.12 is smaller, as twelfths are smaller than sixths | 7.12 is smaller as it has one tenth whereas 7.6 has six tenths | 7.12 |
| 6.4 or 6.8 | 6.8 is smaller, as eighths are smaller than fourths/quarters | 6.4 is smaller as it has four tenths whereas 6.8 has eight tenths | 6.4 |
| 15.3 or 15.30 | 15.30 is smaller as thirtieths are smaller than thirds | They are both have the same value as 3 tenths is the same as 30 hundredths | Both the same |
Write each of the following numbers as fractions and decimals.
Sample answers have been given for the first number.
| Number | Fraction | Expressed as a Decimal |
|---|---|---|
One quarter |  | 0.25, 0.250 ... |
| One eighth | ||
| Three eighths | ||
| One tenth | ||
| One fifth | ||
| Three fifths | ||
| One third | ||
| Two and six tenths | ||
| Twelve and three quarters | ||
| Fifty and a half |
Click here (PDF 280.0 KB) to check your answers
Write each of the following numbers in expanded notation, renaming in terms of the place value parts:
a) 25.6
b) 160.375
c) 3 451.4672
Click here (PDF 241.6 KB) to check your answer
Check your Understanding of Big Idea 2
The purpose of this module was to identify how:
To demonstrate the following understandings:
Does this make sense to you now?
Please continue on with Big Idea 3 in the module, Relationships between Fractions, Decimals, Ratios and Percentages
The learning activities in the previous two modules focussed on numbers represented as fractions , decimals and ratios. This module focuses on percents, another way of representing rational numbers.
Any rational number, whether a fraction or a whole number, can be written as a fraction, decimal or percent.
The term percent is simply another name for hundredths and as such percents are rational numbers with a denominator of 100. For example, 25% (twenty five per cent) is the same as
(twenty five hundredths). 25% orcan also be written in decimal notation as 0.25 (zero point two five).
By the end of this module you should be able to fill in a chart similar to this one.
|
Number |
Fraction |
Decimal |
Percent |
|---|---|---|---|
|
five |
|
5.0 |
500% |
|
two and one eighth |
|
2.125 |
212.5% |
|
three quarters |
|
0.75 |
75% |
Please go to the link below and complete the activities suggested below.
Activities to demonstrate the relationship between fractions, decimals and percents, and reinforce and extend your understandings of percents being another way to represent fractions:
1. Place your curser on the pizza at the 3 o’clock position, or 90 degrees. At this position one whole pizza is shown, the 100 grid is fully shaded (100 percent or 100%) and the number one is identified on the zero to one number line.
(one whole) = 100% (one hundred out of one hundred equal parts) = 1
2. By rotating the curser in an anti-clockwise direction around the pizza, shading the grid or moving along the number line, you can select a portion of the pizza.
Shade one of the 100 squares on the grid. This is one out of 100 equal parts, therefore, 1% (per cent) of the grid. Notice that one hundredth of the pizza appears, and the pointer is a very small distance past zero on the number line.
Imagine the number line from zero to 1 divided into one hundred equal parts. One of these parts is one hundredth, or 0.01. This part is also one tenth of a tenth, or one tenth of 0.1.
(one one-hundredth) = 1% = 0.01 (zero point zero one)
3. Highlight the top row of the grid, that is, ten of the one hundred squares. You have highlighted one tenth of the square, and will notice that one out of ten equal parts of the pizza has appeared. The pointer shows one tenth, or 0.1 (zero point one) on the number line. This can also be written as 0.10, showing that one tenth is exactly the same as ten hundredths. and 10/100 are equivalent fractions (add link – FDRP LO1).
(one tenth) = 10% = 0.1 (zero point one)
4. Move your curser to show:
(one half) = 50% = 0.5 (zero point five) or 0.50
(one quarter) = 25% = 0.25 (zero point two five)
(seven hundredths) = 7% = 0.07 (zero point zero seven)
(three quarters) = 75% = 0.75 (zero point seven five)
(seven hundredths) = 7% = 0.07 (zero point zero seven)
(nine tenths) = 90% = 0.9 (zero point nine) or 0.90
(ninety nine hundredths) = 99% = 0.99 (zero point nine nine)
A one thousand grid can be used to represent one whole (1), and to demonstrate decimals up to thousandths.
The entire grid represents one (1), or one whole.
The grid can be divided into 10 equal parts, or tenths. One of these ten equal parts, or one tenth of the grid (), is shaded in red.
One tenth, the red portion, can be divided into ten equal parts (the yellow section shows this). The yellow portion is a one hundredth () as 100 of these make the whole.
A one hundredth (), the yellow portion, can also be divided into ten equal parts (the blue section shows this). The blue portion is represents one thousandths () of the whole, as 1000 of these thousands makes the whole.
The following statements can be made:
) or zero point one (0.1) of the whole grid
) or zero point zero one (0.01) of the whole grid
) or zero point zero zero one (0.001) of the whole grid
= 1)
= 1)
= 1)
; 0.10 = 0.1
; 0.010 = 0.01
; 0.100 = 0.1
) of the grid, which can also be expressed as the decimal fraction zero point one one one (0.111)
One tenth + one hundredth + one thousandth
(
) or (0.1 + 0.01 + 0.001) or (
) or (
)
The following video uses a thousandths grid in a similar way, to demonstrate writing decimal fractions:
The second example in the video focuses on the shaded area being 500 one thousandths of a whole 1000 (comprising one thousandths). It is written as
or 0.500.
It is easy to see that this shaded area is one half of the whole grid.
This shaded area can also be broken up into 50 hundredths. The fraction 50 hundredths (
) is equivalent to 500 thousandths ().
Furthermore, the shaded area in the video can be broken up into five tenths. The fraction five tenths (
) is equivalent to the fraction 50 hundredths () and 500 thousandths ().
All of these fractions have the same value of one half (), and so they are equivalent fractions.
Decimal notation
0.5 = 0.50 = 0.500
The decimal notation does not require the zeros after the five. Unlike whole numbers, a zero on the end (right hand side) does not change the value of the decimal. However, the zeros can sometimes assist when adding and subtracting decimals.
Click on the following link from Illuminations Resources for Teaching Math:
Follow these instructions:
, a mixed number () , a decimal (1.6667), and a percent (166.67%). Note that the decimal and percent have been rounded up; otherwise they would go on forever.The number line below is marked in increments of one hundredths from zero to 0.36. Notice where the following decimal numbers, all containing similar digits but in different places, are placed on the number line:
|
0.257 |
0.05 |
0.023 |
0.307 |
0.175 |
0.12 |
|---|
The decimal 0.023 has a zero in the tenths place, so it is less than one tenth (0.1). It decimal 0.023 has two hundredths. It also has 3 thousandths, so it is just past the 2 hundredths mark (three tenths past the mark).
The decimal 0.05 has a zero in the tenths place, so it is less than one tenth (0.1). is bigger than 0.023, as it has more hundredths.
The decimal is 0.12 has 1 tenth and 2 hundredths, so is two hundredths past the one tenth (0.1) mark.
The decimal 0.175 is also between 0.1 and 0.2, but it is closer to 0.2 because it has seven tenths. It is half way between the seven and eight tenths marks because it also has 5 thousandths.
The decimal 0.257 is between 0.2 and 0.3. It has five hundredths, so it is about half way between 0.2 and 0.3. It also has 7 thousandths, so it is just past half way between 0.2 and 0.3.
The decimal 0.302 is only 2 thousandths more than 0.3, so it is only slightly past the 0.3 mark.
This time the three different representations of rational numbers, fractions, decimals and percents, have been placed on a blank number line.
|
15% |
0.28 |
|
70% |
0.115 |
1 |
|
|
0.3 |
|---|
|
15% |
0.28 |
|
70% |
0.115 |
1 |
|
|
0.3 |
|
|
|
|
|
|
|
|
|
|
* 
and
are close approximations. The decimal 0.115 is actuallyand 5 thousandths and is a little more than, because it is 0.3333333.
Examples of how percentages are used in real life
Example 1
. We can then work outof $130 which is $32.50.Example 2
A property that was on the market for $450,000 last year has decreased in value by 10%. How much will you save by buying it now?Solution: We recognise that 10% is the same as. Nowof $450,000 is $45,000. Therefore you would save $45,000 by buying the property now.
(Note that a 10% discount off a small item such as a $20 t-shirt amounts to just a few dollars, in this case $2. Whereas a 10% discount of a $450,000 property is a very worthwhile $45,000. So the significance of what a 10% discount might mean to us depends on the whole we started with).
Decimals stop at hundredths - NO
Examples of decimals beyond hundredths:
A millimetre (mm) is one thousandth of a metre
1mm = 0.001m
2.44 micrograms is equal to 0.00244 milligrams.
1. The larger the denominator, the bigger the fraction
This is true for unit fractions (fractions with a numerator of one). There is an inverse relationship between the number of parts and the size of each part: The larger the number of parts (the denominator), the smaller the size of each part (the numerator). Unless the problem context indicates that two fractions relate to different wholes, we assume both relate to the same whole. With this in mind, it makes sense that the more parts into which the whole is divided, the smaller they will be.
Example: Compare one eighthto one fifth
If we are referring to the same whole, such as a portion of a cake (modelled below), we can see that the more parts into which it is divided, the smaller each part will be.
In the visual representation, we can clearly see thatis larger than.
Five people sharing above cake, soeach
Eight people sharing same sized cake, soeach.
When we are comparing just one of each part, such as one eighthto one fifth (), the bigger the denominator, the smaller each part will be.
The numerator is one (
)
When one or both fractions are not unit fractions:
This time, we will compare one fifth(), and three eighths (
). We know that eighths are smaller than fifths, but we must note that this time there are three eighths, not just one.
In the diagram below, we can see thatis a bigger portion than.
Person A ate one fifth () of the cake.
Person B ate three eighths () of the cake.
If we cannot reliably compare the fractions with different denominators visually, as in the diagram above, we need to change one or both of the fractions into equivalent fractions for a common denominator.
It is easy to recognise that four fifths () is greater than two fifths (), because each of the parts (fifths) is the same size. Four is greater than two, somust be greater than .
What about comparing four fifths () and seven tenths (
), which have different denominators?
As was seen on the fraction wall, each fifth is equivalent to two tenths. This is demonstrated in the model below:
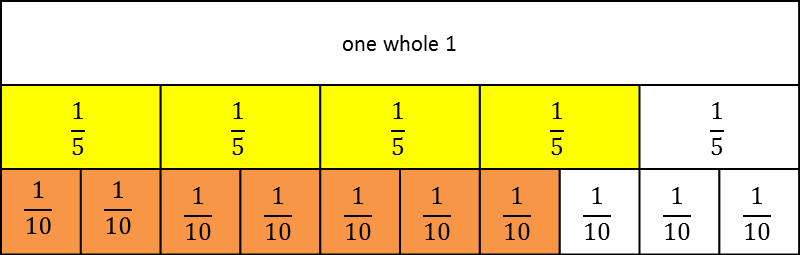
Changing four fifths () to the equivalent fraction eight tenths (
) makes it much easier to see that four fifths () is greater than seven tenths ().
1) Complete the table so that the numbers in each row represented by fractions, decimals and percents are equivalent:
Fraction | Decimal | Percent |
|---|---|---|
| 1.1 | 110% |
| ||
0.04 | ||
25% | ||
| ||
350% | ||
0.125 |
2) Order the following numbers from smallest to largest:
0.125
1.5
1.45
0.25
0.81
0.09
1.1065
3) Write at least four equivalent fractions for each of the following fractions:
|
|
|
Click here (PDF 362.6 KB) to check your answers
1) Relating decimals, fractions and percent using a number line
Click on the link below and complete the activity by placing all of the fractions, decimals and percents on the number lines from ICT games.
2) Place the following fractions, decimals and percents on a single number line:
10%
0.375
50%
1.3
128%
0.002
3) Take a look in the day's newspaper and highlight every time percentages are referred to or used. This is an activity that students could do as well.
Click here (PDF 275.9 KB) to check your answers
The purpose of this big idea was to demonstrate the following understandings;
Does this make sense to you now?
Please proceed to Big Idea 4 in the Relationships between Fractions, Decimals, Ratios and Percentages module.
Using percent in to solve everyday problems requires proportional reasoning. Proportion reasoning involves the consideration of number in relative terms,rather than absolute terms.
For example, converting a fraction of
(five sixths) to a percent is equivalent to finding what part of 100 is equal to five parts out of six.
In numerical notation this can be expressed as
One way to convert a fraction into a percent is to remember that any fraction can be interpreted as a quotient (division) (see FDRP BI2 Fractions as division). In the case of, this is 5 ÷ 6. Using a calculator, 5 ÷ 6 is
. Remembering that percents are hundredths, this can be expressed as
.
Knowing this can make understanding of everyday maths language easier, such as in the following example of percent decrease.
Example 1
Mathematical language and data presented in media is not always clear. Being able to understand percent use and its relationship with fractions, decimals and proportional reasoning helps us to more easily interpret information about our world.
So do you think that an increase in the number of deaths by drowning from 57 to 64 the following year is an alarming increase?
Click on the following link to read the news story “Drink swim deaths rise”
http://www.mercurynie.com.au/mathguys/mercury.htm
Click on data representation and then on the article "“Drink swim deaths rise”
The second paragraph refers to percent increase:
Alarming figures show a 12.3 per cent increase in drowning deaths in the 25 to 34 year old age group, and 90 per cent of the deaths were male.
The 12.3% increase in drowning in the 25 – 34 age group is referred to as ‘alarming’ by the reporter, but for a clearer perspective we would have to know the actual numbers.
The graph in the article shows the number of drowning for each age group, which totals 292, as mentioned in the article. The number of drowning in the 25 – 34 age group is the highest on the graph, and appears to be about 64 in number. This number of 64 includes the 12.3% increase, so the 64 is comprised of the previous year’s 100% plus the 12.3% increase. Therefore the number 64 represents 112.3% of the previous year’s number of deaths by drowning in the 25 -34 age group.
To work out 1% of 64, we can divide 64 by 112.3 to get 0.5699. We can therefore workout that in the previous year 57 people (100 x 0.5699) drowned and that in the following year 57 + 7 more (12.3 x 0.5699) people drowned. Note that in a context like this in which the numbers calculated are numbers of people, rounding to the nearest whole number is appropriate.
Example 2
Image provided by: Mathematics Assessment Resource Service
Take a look at the money cards above and consider the following:
% (33.83 ̇%)
Example 3
A few years ago, a Tasmanian politician was up in arms about the drop in poker machine profit tax from 6% to 1%. He said that the taxed had dropped by 500%.
A solid understanding of percent would help recognise that because 100% is the whole, any decrease of more than 100% would not make sense as it would result in a negative. In other words, If the drop was 100%, the tax would be zero.
It is important to consider that a change in percent is always considered in relation to the original amount. The tax dropped from 6% (the original whole amount of tax) to 1%, so it dropped by five out of six. From our previous calculation, we know thatis .
We can see that the actualdecrease is a considerable drop in tax.
http://www.mercurynie.com.au/mathguys/mercury.htm
The 1996 news story “Drink swim deaths rise” also contains an example of use of percent to make comparisons. Look at the same paragraph as the previous section:
Alarming figures show a 12.3 per cent increase in drowning deaths in the 25 to 34 year old age group, and 90 per cent of the deaths were male.
As well as the mention of a 12.3% increase, percent is used to highlight the number of male deaths compared to female deaths.
In the previous section we calculated the number of deaths for two consecutive years, being 57 and 64. Using knowledge of percent or fractions (in this case hundredths) as an operator (see FDRP BI2 Fractions as operators), we can work out the numbers of males and females for a clearer understanding of the data. Again, in this context where the numbers calculated are numbers of people, rounding to the nearest whole number is appropriate.
|
Total Number of Males and Females |
Approximate Number of Males |
Approximate Number of Females | |
|---|---|---|---|
|
Year A |
57 |
51 0.9 (90%) x 57 = 51 |
6 0.1 (10%) x 57 = 6 |
|
Year B |
64 |
58 0.9 (90%) x 64 = 58 |
6 0.1 (10%) x 64 = 6 |
The actual numbers of male and females who drowned, rather than using percents, may send a clearer message than percents about the difference between male and female drownings.
When money is borrowed or invested for a fixed time at a fixed interest rate and the interest rate is calculated only on the initial investment, simple interest (sometimes known as flat interest) is calculated. (Note: that simple interest is not the only way that interest can be calculated).
The following formula is useful for calculating simple interest:
I = P x R x T
where; I = Amount of interest, P= Principal (Amount invested or borrowed), R= Interest rate per annum (per year) as a decimal eg: 5%=0.05 and T= Time of investment in years
(Note also that in an algebraic formula like this we do not need to put in the multiplication symbol. We can just write I =P R T)
You may have also seen this formula written like this:
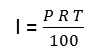
For example if the interest rate was 5% you would enter a 5 in place of the r so you would have 
( note that the 
part is already in the formula)
Either form can be used, it is your own personal preference.
Please refer to Examples 4 and 5 below for some worked examples of simple interest calculations
Example 1
Your weekly pay of $748 will increase by 3.5%. What will your new weekly pay be?
Sample solving strategy:
| Step 1. Find 1% x 748. 1% = |
x 748 = 7.48 (748 ÷ 100) |
| Step 2. The pay rise is 3.5% which is half of 7%. Multiplying by 7 and halving the product is a helpful mental strategy if no calculator is available. |
( 7 x 7.48 = 52.36 |
| Step 3. Add the pay increase to the original whole. |
$748 + $26.18 = $774.18 |
If a calculator is available, use the fraction as an operator method:
x 748 = 0.035 x 748
0.035 x 748 = 26.18
748 + 26.18 = $774.18
Example 2
The average price of bread increased from $2.80 to $3.70 over three years? What was the percent increase?
Sample solving strategy:
The price increase was $3.70 - $2.80 = 90c
Therefore the price increase is 0.9 out of the original 2.80
0.9 ÷ 2.8 = 0.32
0.32 = 32% price increase
Example 3
You need to borrow $5,000. What is the best two-year deal, A or B?
|
Deal A Pay back with 12.5% interest within two years. |
Deal B Pay back half ($2 500) interest free within 6 months, then the rest at 30% interest. |
|
Deal A sample solution strategy: 12.5% is half of 25% Pay back $5 000 + $625 = $5 625 |
Deal B sample solution strategy:
Pay back $2 500 + $2 500 + $750 Pay back $5 750 |
So deal A is the best deal.
Example 4
$4200 is invested at 5.2% pa. flat for 18 months
How much interest does it earn?
What is the total amount returned to the investor?
Solution
P = 4200
R = 5.2% = 0.052
T = 18 months = 1.5 years
So since I = PRT
I = 4200 X 0.052 X 1.5
I = 327.6
Therefore the interest earned is $327.60
Total in the account = 4200 + 327.6 = $4527.60
Example 5
Find the interest charged if a loan of $7000 is made for three and a half years at 12% flat.
Solution
P = 7000
R = 12% = 0.12
T = 3.5 Years
So since I = P R T
I = 7000 x 0.12 x 3.5
Therefore I = $ 2940
You want to buy two T-shirts. Which is the best buy, Shop A or Shop B?
Shop A. Buy two Bonds Tees at $25 each and get 30% off the second T-shirt. | Shop B. All Bonds Tees 25% off normal price of $30 each. |
Click here (PDF 358.7 KB) to check your answer
A survey of 1000 females showed that the number of smokers increased by 8% over two years. In the original survey, the number of smokers was 238. What was the number of smokers after 2 years?
Click here (PDF 277.0 KB) to check your answer
The staff of a company decreased from 55 to 25. What was the percent decrease?
Click here (PDF 274.1 KB) to check your answer
John paid $14 000 for his car. This price included 15% sales tax. What was the actual price of the car before sales tax?
Click here (PDF 171.6 KB) to check your answer
Find the interest charged if a loan of $ 9500 is made for 2years at 11.5% flat.
Click here to check your answer
The previous module showed how percents are hundredths and as such are another way of representing rational numbers. However, learning with relation to percent cannot be limited to this understanding, but must also be linked with proportional reasoning as well as decimals and fractions.
Percents are frequently used in real life situations such as when working with interest rates, discounts and price changes. Percents are also often used to compare two quantities.
The purpose of this module was to further develop your knowledge of the meaning of percent by exploring how percents can be used in real life contexts.
If you have completed all the Big Ideas and feel you have a good understanding of each Big Idea, then test yourself with the module Quiz for the Relationships between Fractions, Decimals, Ratios and Percentages
Click here to take the Quiz
Good Luck!!
)