UTAS Home › › Mathematics Pathways › Pathway to Education › Measurement
In everyday life, we often use non-standard or informal units of measurements such as paces for distance or cups for cooking. When teaching children, it is beneficial to use non-standard units in the initial development of understandings about measurement for a number of reasons:
The following link shows you some non-standard units used as long ago as ancient Egyptian times and explains the need for the use of standard units. It also shows how the base 10 decimal system or metric measurement is easier than the imperial measures of the U.S.A.
A measurement investigation using non-standard units of different sizes promotes awareness of the importance of universal standards of measurement, such as metres, where the unit of measurement is always the same.
Here is a quick example…

Clipart of Pirates
The need for precision requires the use of a standard unit. It may be okay to measure your lawn for grass seed using paces and approximation, but measuring to install a window would require a high level of precision.
To use standard units effectively, it is important to:
In Australia and most parts of the world the metric system for measurement is used. The following chart shows the measuring units used for length, mass and volume, and their abbreviations.
|
Length |
Mass |
Volume |
|---|---|---|
|
millimetre (mm) |
milligram (mg) |
millilitre (mL) |
|
centimetre (cm) |
gram (g) |
litre (L) |
|
metre (m) |
kilogram (kg) |
kilolitre (kL) |
|
kilometre (km) |
tonne (t) |
|
These metric units are based on multiples of 10 (see Place Value BI1), as can be seen in the following table:
|
Length |
Mass |
Volume |
|---|---|---|
|
10 mm = 1 cm |
1000 mg = 1 g |
1000 mL = 1 L |
|
100 cm = 1 m |
1000 g = 1 kg |
1000 L = 1 kL |
|
1000 mm = 1 m |
1000 kg = 1 t |
|
|
1000 m = 1 km |
The information in the table above can be used to convert from one unit to another, for example:
Not all measurements in Australia are metric. Some measurements still use the old imperial system of yards, feet and inches, and pounds and ounces. For example, air pressure in tyres is still commonly measured in pounds per square inch. When you pump your tyres to a pressure of 35 you are actually making the pressure in your tyres 35psi meaning 35 pounds per square inch.
It is not convenient to use metric units for all measures of time. Units of measurement for time include seconds (s), minutes (min), hours (h), days (d), months (mo), years (yr), decades, centuries and millennia (plural of millennium). The table below shows some of the relationships between units of time measurement.
|
Time |
|---|
|
60 s = 1 min |
|
60 min = 1 h |
|
24 hr = 1 d |
|
365.25 d = 1 yr |
|
12 mo = 1 yr |
|
10 yr = 1 decade |
|
100 yr = 1 century or 10 decades |
|
1000 yr = 1 millennium |
Some people experience confusion when they come across certain terms that measure time in historical accounts. Here are two:
The “BCE and CE” abbreviations are used in some books instead of the “AD & BC” abbreviations.
AD & BC are Christian calendar concepts.
AD – anno domino (Latin) and means in the year of our Lord.
BC- before Christ
Some people prefer to use terms that are more inclusive of non-Christians. Instead of saying AD, they use “CE” which is short for “Common Era” of “Current Era” and instead of using BC, they write BCE which means “Before the Common Era” or “Before the Current Era”.
Interestingly, there is no year “zero” in our timeline. The year 1BC (or BCE) is followed by the year 1AD.
What do we mean by the 16th century?
Periods of 100 years can be referred to in two ways. We talk of the 1600s which means the years that begin with “16” e.g., 1610, 1634 etc. We also talk of the 16th century. The 16th century is those years that begin with “15” e.g., 1540, 1583. The 1600s are not the 16th century.
What century are we in now?
What are the first two digits of the years in the century we are in now?
Temperature can be described the degree of hotness or coldness of something. The higher the temperature the hotter it is, and conversely, the lower the temperature the colder it is.
Attempts at standardising temperature measurement were made as early as 170 AD. The first sealed thermometer was constructed in 1641. In the 1700's Gabriel Fahrenheit made a thermometer using mercury and a scale known as the Fahrenheit scale, which is still used today. Fahrenheit set the freezing point of water at 32 degrees (°) and the boiling point at 212 degrees. You may have noticed Fahrenheit temperatures used on older ovens and in recipes. The chart below shows the Celsius oven temperatures and the equivalent Fahrenheit measures.
Degrees Celsius | Degrees Fahrenheit | Description |
|---|---|---|
110 | 225 | very cool |
130 | 250 | |
140 | 275 | cool |
150 | 300 | |
170 | 325 | moderate |
180 | 350 | |
190 | 375 | moderately hot |
200 | 400 | |
220 | 425 | hot |
230 | 450 | |
240 | 475 | very hot |
Around 1743, Anders Celsius (1701-1744) invented the Celsius scale. Based on Fahrenheit's measures, Celsius established the freezing temperature for water to be 0 degree and the boiling temperature 100 degrees. The Celsius scale is known as a Universal System Unit. Australia and most parts of the world now use this metric system for measurement.
The 'number line' for measuring temperature is vertical and includes negative numbers (below zero). The thermometers below show Fahrenheit, Celsius and Kelvin scales.
The Kelvin scale is a less common measure of temperature. There is a limit to how cold something can be and the Kelvin scale is designed to go to zero at this minimum temperature.
The relationships between the different temperature scales can be seen on the thermometers below:
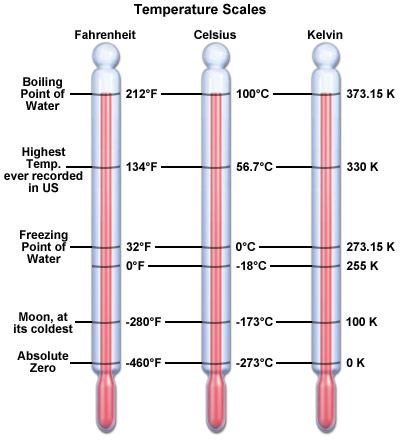
Temperature is important as it is something we feel. The temperature can determine life or death of animals and plants.
We need to be aware of temperature and be able to measure temperature for many reasons and to solve many problems:
Click on the link below to use the interactive thermometer by dragging the slider from Math Is Fun - Maths Resources website. Take note of how Celsius and Fahrenheit temperatures are recorded, and discover the temperature of a range of objects from freezing wind and snow in a blizzard to boiling water. Did you know that heating cow’s milk to a temperature of 80°C or more will burn the milk? Soy milk would burn at an even lower temperature of about 70°C.
Click on the link below to estimate and discover the temperature of objects from planets to super fluid helium. Use the Celsius temperature scale.
Convert the following measures to the alternative unit that can be used to measure the same attribute.
|
Attribute |
Measure |
Alternative Measure |
|---|---|---|
|
Length |
1500 m |
? km |
|
Length |
62.5 cm |
? mm |
|
Mass |
1400 g |
? kg |
|
Mass |
1.1 t |
? kg |
|
Volume |
0.75 L |
? mL |
Click here to check your answers
Viewing the thermometer as a vertical number line will assist with calculating the change in temperature.
For example, a temperature change from 12°C to -10°C is a drop or fall in temperature of 22°C.
| A drop from 12°C to zero is 12°C. A further drop from zero to -10 is 10°C. The total drop in temperature is 12 + 10 = 22°C |
|
a) from 22°C to 13°C
b) from 37°C to 40.5°C
c) from 16°C to -3°C
d) from 85°C to 16°C
e) from 180°C to 85°C
f) from -5°C to -36°C
Click here (PDF 166.4 KB) to check your answers
What is 20/20 vision?
This is a measure that indicates the sharpness or clarity of vision at a distance. It means you can see clearly at 20 feet (imperial system of measurement) what should normally be seen at that distance. If you have 20/100 vision, it means that you must be as close as 20 feet to see what a person with normal vision can see at 100 feet.
The metric equivalent is 6/6 (metres). A person with 6/30 vision means that you must be as close as 6 metres to see what a person with normal vision can see at 30 metres. It is measured using a Snellan chart (after a Dutch ophthalmologist) which has a series of letters of different size in rows.
Decibels and your hearing
Preserve your hearing: Noise level is measured by the magnitude of sound pressure. The range of sound pressures commonly encountered is very large so a logarithmic scale is used. The decibel is the unit used on this scale and is abbreviated to dB.
On the decibel scale, the threshold of hearing occurs at a sound pressure level of about 0dB and the threshold of pain occurs at about 120dB. Human speech is around 35-45 dB, using a vacuum cleaner is less than 90 dB; operating a drill is 95-100 dB, and a rock concert is about 120-130 dB.
A KISS concert in Canada in 2009 was measured at 136 dB by local government officers, making it the loudest officially measured band in the world.
Here is a list of the top 10 loudest noises
The aim of this Big Idea was to develop the following understandings;
Does this make sense to you now? If so, continue on with Big Idea 2!
To select the correct unit for measuring, an understanding of the attribute to be measured, and the context, is required. For example, the linear (one-dimensional) measurement of metres is required for measuring the attribute of length in the case of a race on a school oval and the measurement unit of kilometres is more appropriate for measuring the distance run in a marathon.
When measuring the attribute of area in the case of the lawn coverage that a particular amount of pesticide covers, the two-dimensional unit of square metres is appropriate. However, when measuring the area that a bushfire has destroyed, the two-dimensional unit of hectares (100 metres by 100 metres) or even square kilometres (1 kilometre by 1 kilometre) is appropriate.
When measuring the attribute of volume, a three-dimensional unit is required. For example, the amount of petrol to fuel up might be measured in litres but the amount of concrete needed for a driveway will be measured in cubic metres. Once a unit is chosen, the same unit must be used throughout the entire measuring task.
Once a unit is chosen, the same unit must be used throughout the entire measuring task. It would be difficult to calculate how many centimetres of elastic are needed to go around a 34 inch waist, or how many square centimetres of paint are needed for an eight square metre wall. In both cases, a conversion would be required.
Unit iteration is the repetition of a single unit of measurement. For example, if you are measuring the dimensions of a room with a measuring tape, units such as millimetres, centimetres and metres are repeated, side by side with no overlapping, on the tape.
However, if you were measuring the room with a one metre ruler, you would need to iterate or repeatedly reposition the unit (metre ruler), checking that the length of the ruler is exactly one metre from end to end. Remember that spaces on some rulers may not be covered by a unit of measurement, such as a gap before the zero at the beginning of the ruler or a gap after the 1 metre mark.
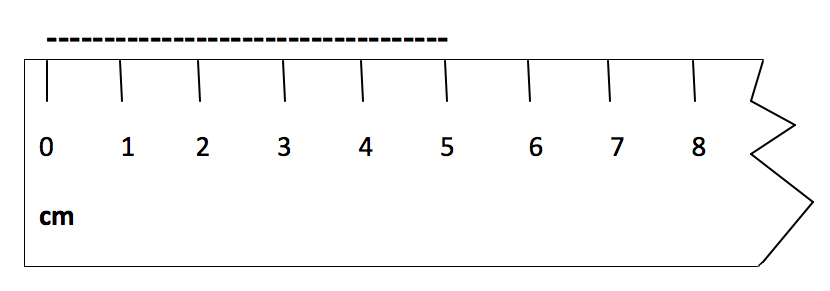
The diagram below shows an example of a space on a ruler to the left of the “0” mark not covered by a unit of measure (cm). This has been considered so the line could be correctly measured as 5 cm in length.
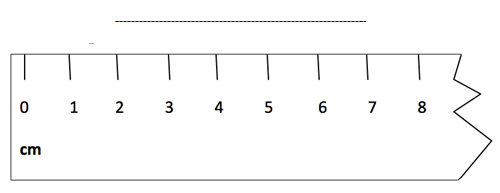
The line in the above diagram need not have been measured on the ruler starting at zero. The diagram below shows how the measurement is not a position on the ruler, but rather it is a space between the markings. The line is still a length of 5 cm, the space from the 2 cm to 7 cm markings.
Even if an appropriate unit of measurement or tool has been chosen, measurements are always approximations.
Unlike number counts which are exact, such as ’12 eggs’, measurements are never exact. You may say you are 167 cm tall, but this is an approximation as you are unlikely to be exactly 167 cm tall.
Measurement of length
When we are measuring the extent or distance of something from end to end we are measuring length. The following are examples of length:
We also measure the length of time from start to finish of a race. Time is a different quantity from the quantity measured in the above four examples.
1. Choose the most appropriate unit of length from millimetres (mm), centimetres (cm), metres (m) and kilometres (km) for the following tasks. Think about where precision is important.
a) Measuring the length of timber when constructing a picture frame.
b) Measuring the space between vegetable seedlings when planting.
C) Giving directions for driving from Sydney to Melbourne.
d) Measuring a length in your backyard to set up a cricket pitch for a family game.
2. Measure the length of a sheet of A4 paper. Give the answer in:
a) millimetres
b) centimetres
c) metresClick here to check your answers
Area is the two-dimensional space within a boundary. This is not to be confused with perimeter, which is the length of the boundary.
 In the photograph, the area is the size of the horse paddock. The length of the fence enclosing the paddock is the perimeter.
In the photograph, the area is the size of the horse paddock. The length of the fence enclosing the paddock is the perimeter.
Image: My Builder
Square units are required when measuring an area. Completely covering an area with iterated square units without gaps or overlaps can be more difficult than repeating a unit of measurement along a length, especially when the area to be covered and measured is irregular. See Measurement
BI3, measuring in whole units and parts of units.
The following video will show how using square tiles or units allows an area to be covered without gaps or overlap. Watch only as much as you need.
The area of the shaded shapes below is the number of square units (units2) that are shaded.
The shaded areas may be different shapes, but they all have as area of 8 square units.
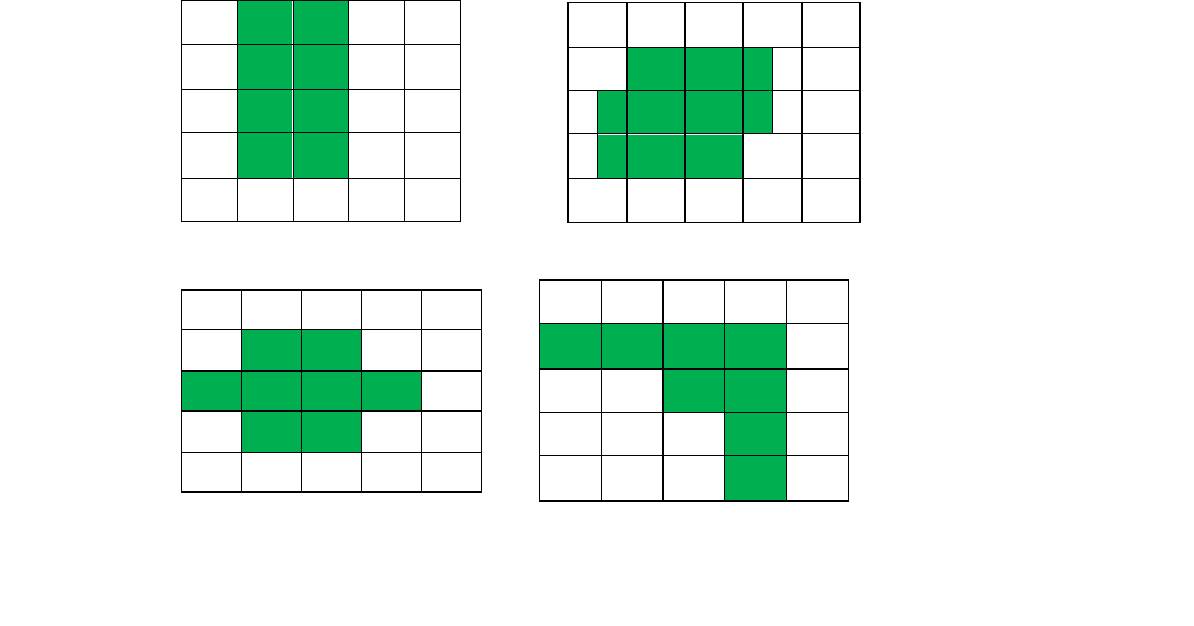
Practice Task
What is the area of the following outlined shapes?
a)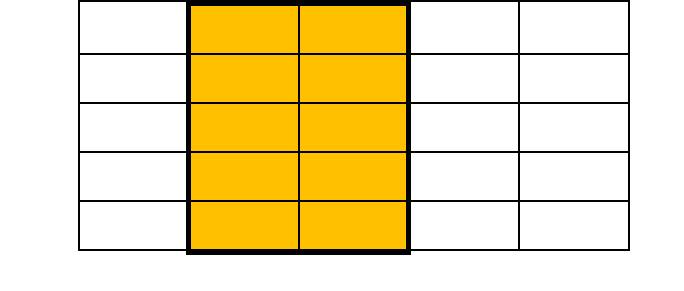 b)
b) 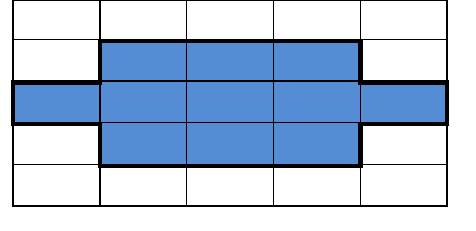
c) 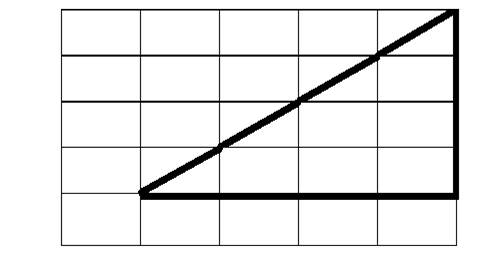 d)
d) 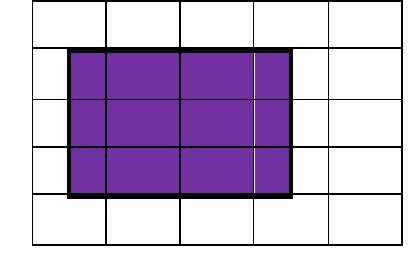
Click here to check your answers
When we want to calculate the areas of regular shapes such as squares, rectangles, triangles, circles or combinations of these shapes, formulae are often used. This makes the calculation much more efficient than counting square units!
The area of a rectangle is calculated by multiplying the length of the base by the length of the height. When written as a formula we say A=bh (note there is an “invisible” multiplication sign between b and h) where b is the base and h is the height of the rectangle. Sometimes the formula is written as A=lw where l is the length and w is the width of the rectangle.
Example 1
The area of the following shape is 3 x 8 = 24cm2.
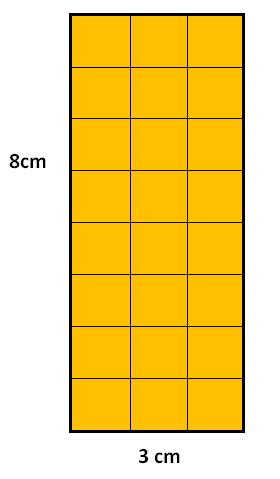
Example 2
How to solve an area problem that involves more than one calculation..
Find the area of the shaded region:
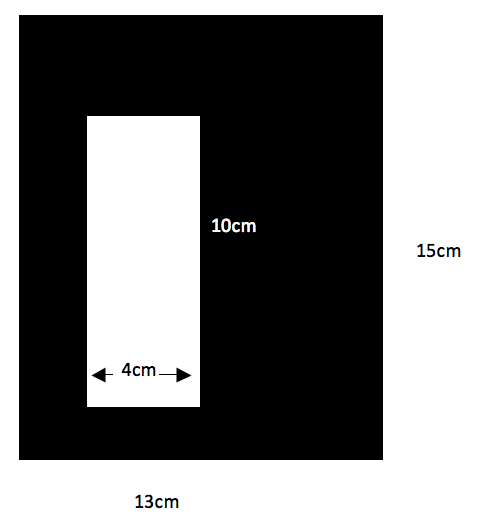
The area of the shaded area can be found by subtracting the area of the inner rectangle, which is 40 cm2 (4 x 10), from the entire area which is 195 cm2 (13 x 15).
Therefore the area of the shaded area is 155 cm2.
Practice Task
Find the area of the blue, red and white regions?
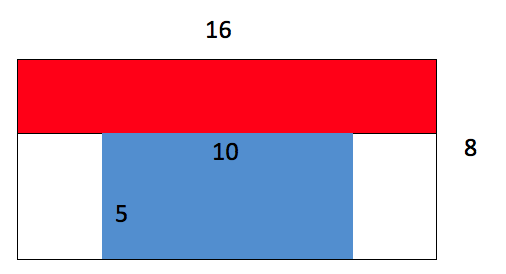
Click here to check your answers
Open the link below and go through the explanations and practice examples for calculating perimeter and for calculating area. Start with level one to check your understandings, and continue through to the next levels to build on understandings.
The area of a rectangle can sometimes be used to work out the area of a triangle.
Acute-angled triangles are those with all three angles less than 90°. They can be placed in a rectangle whose length is the same as the base of the triangle and whose width is the same as the height of the triangle.
In the diagram below you can see how the acute-angled triangle XWY is half the area of the rectangle XWYX', and that the acute-angled triangle WZY is half the area of the rectangle WZZ'Y.
Therefore, to find the area of the triangle XYZ, we halve the area of the rectangle X'XZZ'.
The area of a rectangle is base (or width) x height, so the area of a triangle is half the base x height.
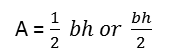
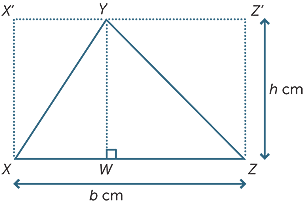
Image source: Australian Mathematical Sciences Institute
Obtuse-angled triangles are those with an angle greater than 90°.
The side BC of the shaded obtuse-angled triangle below has been extended to form a right angle at point D. Now the area of the formed right-angle triangle ADC is half of the rectangle having the same base and height and is calculated by using the formula A = ![]() bh. The the area of the right-angle triangle ADB is half the area of the rectangle that has the same base and height as the triangle. It can also be calculated using the same formula.
bh. The the area of the right-angle triangle ADB is half the area of the rectangle that has the same base and height as the triangle. It can also be calculated using the same formula.
To find the area of the shaded area we subtract the area of the smaller triangle ADB from the area of the larger formed triangle ADC.

Image source: Australian Mathematical Sciences Institute
1. What is the area of the following triangles?
Because the unit has not been stipulated, give your answers as ___ units2
a) 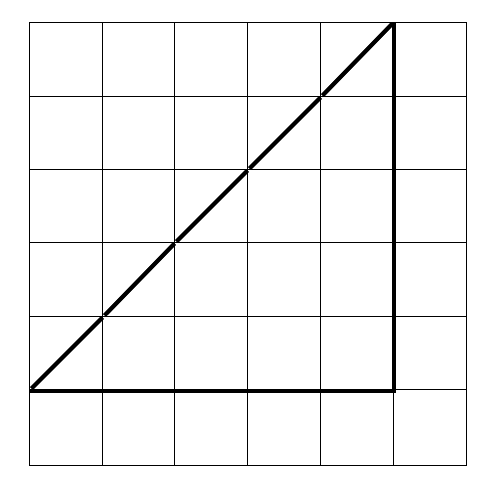 b)
b) 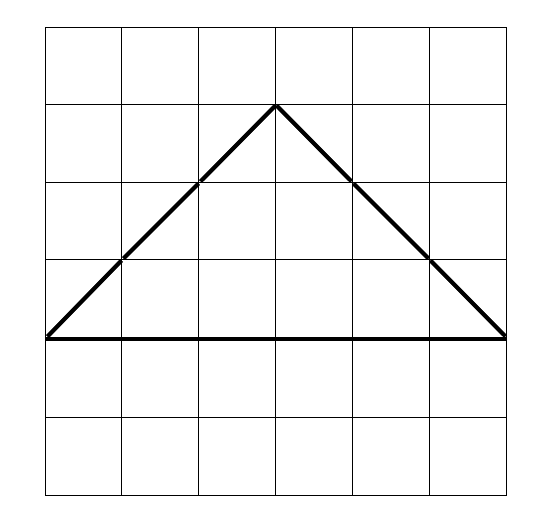
2. What is the area of this acute-angled triangle?
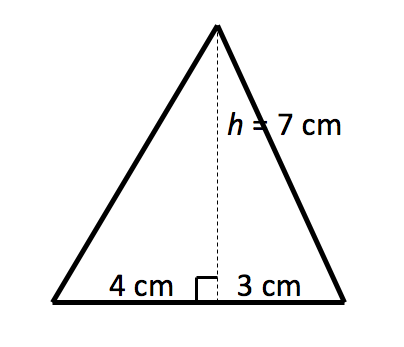
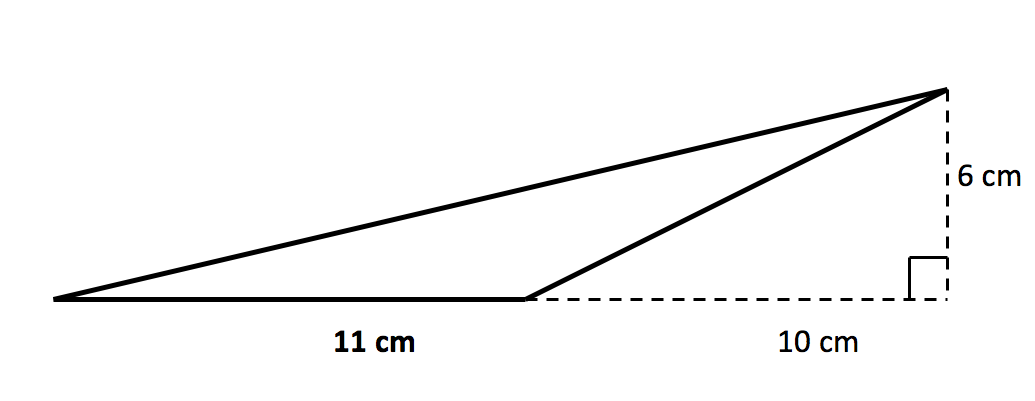
3. What is the area of this obtuse-angles triangle?
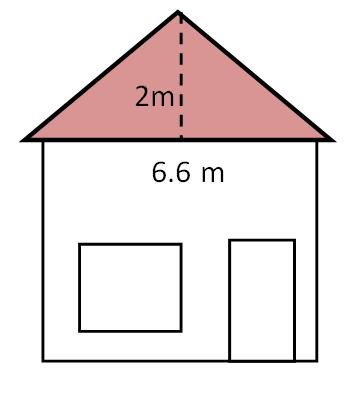
4. Work out the area of the following triangular roof facade to assist with knowing how much paint to buy?
Click here to check your answers
The following shapes all have a perimeter of 16 units. You can check this by finding the sum (total) of the lengths of the sides for each shape.
Count the square units to discover if the area of all of the shapes stays the same.
a)  b)
b)  c)
c)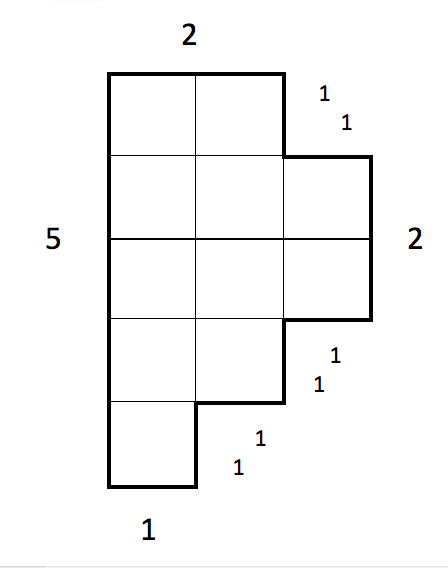
You would have discovered that while the perimeter is the same length in each example, the area is not the same, measuring 16, 15 and 11 square units respectively. Counting the square units in the square (a type of rectangle) and rectangular shapes may have reminded you of the simple rule for finding the area of a rectangle which is multiplying the length by the width. For example, the area of shape b) is found by multiplying 5 x 3 (as there are 5 rows of 3 square units) giving an area of 15 square units.
This time, the following shapes all have an area of 9 square units.
Measure the perimeters of each shape, remembering that each side of the square unit has a length of one unit.
d)  e)
e) 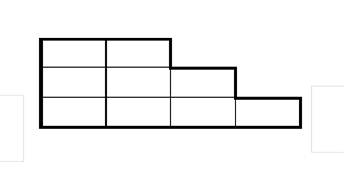 f)
f)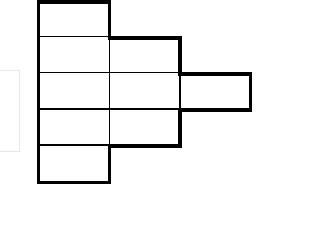
You would have discovered that even though the area remained the same for each shape, the perimeters were 12, 14 and 16 units respectively.
We can conclude that there is no direct relationship between perimeter and area.
Imagine that all of the above shapes a) to f) are pens in need of fencing, and the units of measurement are metres and square metres. We know that the pens a), b) and c) with areas of 16, 15 and 11 square metres all require a 16 metre fence.
The shapes d), e) and f) all with an area of 9 square metres (or 9 m2) require fencing lengths of 12, 14 and 16 metres.
You may have noticed that the square is the most economical shape, providing maximum area for the least amount of fencing.
The perimeter or distance around the edge or boundary of a circle is referred to as its circumference. See Geometry module 1 to learn about the properties of circles including circumference, radius, diameter and area, and how to calculate these properties and the relationships between them.
The volume of a three-dimensional object or substance is the amount of space it takes up. It is measured in cubic units (three-dimensional).
The volume of the rectangular prism below is the number of cubic units (units 3).
Each cube is one unit by one unit by one unit, so the unit for measuring volume is 1 unit3 (pronounced "one cubic unit"). We can see that 4 cubes fit along the length of the rectangular prism and 3 cubes fit along the width, so one layer is 12 cubes. The height of
the rectangular prism is 5 units, hence there are five layers; therefore the volume of the rectangular prism is 60 cubic units (or 60 units3).
In summary, 4 x 3 x 5 = 60 units3

Image source: Australian Mathematical Sciences Institute
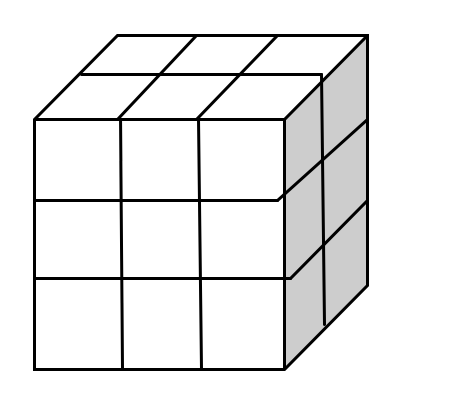
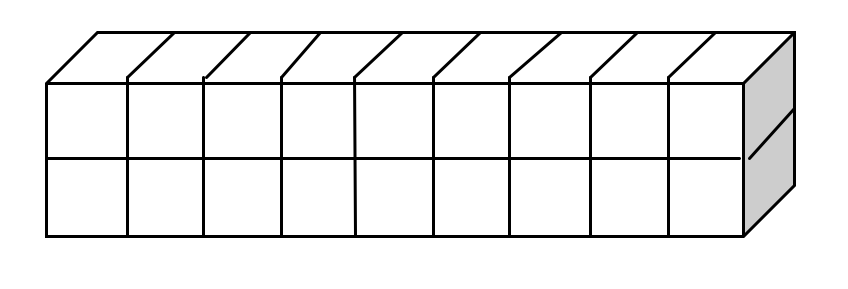
Objects with the same volume may have different shapes.
The rectangular prism to the right has a volume of 18 cm3 (3 x 2 x 3).
The rectangular prism below has a volume of 18 cm3 (9 x 1 x 2).
The outside dimensions of a standard dry cargo container (below) are:
Length: 6.05 m
Width: 2.44 m
Height: 2.5 m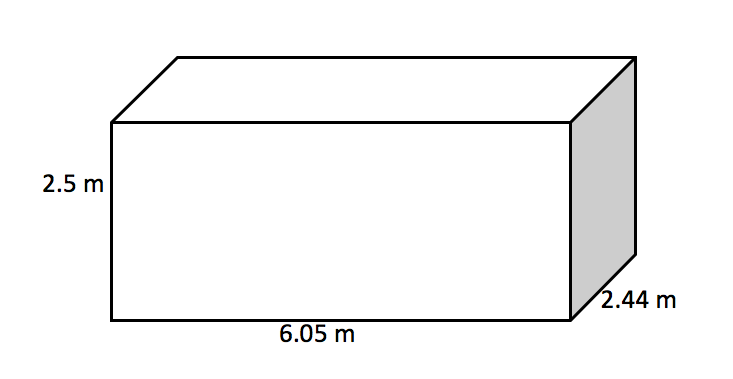
The volume of the container, or the amount of space it takes up, is:
6.05 x 2.44 x 2.5 = 36.9 m3 (correct to one decimal place)
The capacity of a container is how much it holds. The capacity of a standard dry cargo container will be less than 36.9 m3 depending on the thickness of its sides.
The inside dimensions of a standard dry cargo container (below) are:
Length: 5.9 m
Width: 2.35 m
Height: 2.38 m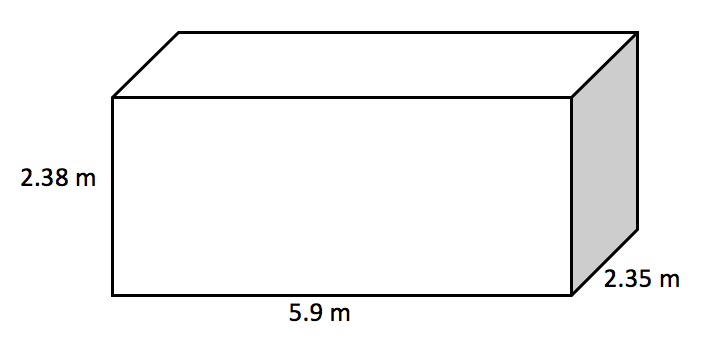
The capacity of the container, or how much it holds, is:
5.9 x 2.35 x 2.38 = 32 m3
As previously demonstrated, the volume of a rectangular prism can be found by multiplying the dimensions:
Volume = Length x Width x Height.
This formula can be rewritten as Volume = Area of Base x Height. This is known as the cross-section method. The formulae are the same because the area of the base is length x width.
The formula Volume = Area of Base x Height applies to all solids that are prisms. A prism has a cross section that does not change along its length. The base of a prism (and therefore its cross section) is a polygon. Do an Internet search for images of prisms. Identify rectangular prisms, cubes, triangular prisms, and hexagonal prisms to name just a few.
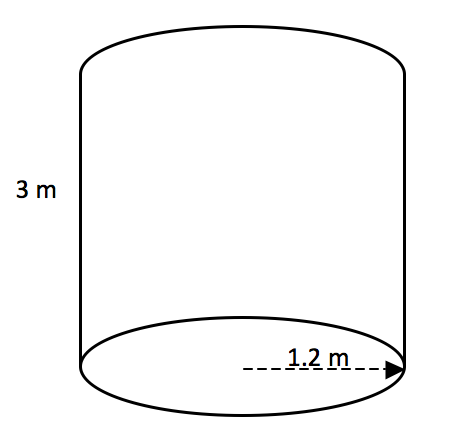
The volume of a cylinder is also given by the formula Volume = Area of Base x Height. Although a cylinder isn’t technically a prism because its base is not a polygon, you can imagine a circle to be a polygon with many, many sides.
To calculate the volume of the cylinder below:
The area of the base, which is a circle, is π r2 (see Geometry Module 1).
The radius of the circular base is 1.2 m, and the value of π is approximately ![]() or 3.14, so the area of the base is approximately: 3.14 x 1.2 x 1.2 = 4.52 m2.
or 3.14, so the area of the base is approximately: 3.14 x 1.2 x 1.2 = 4.52 m2.
To find the volume, the area of the base is multiplied by the height: 4.52 x 3 = 13.56 m3
Volume and Nets (see Geometry module 1 – 3D shapes)
Click on the link from Annenberg Learner below to complete the volume activities titled
Click on the solution boxes on the activity page to check your answers.
1. Find the volume of the following prisms?
a) rectangular prism 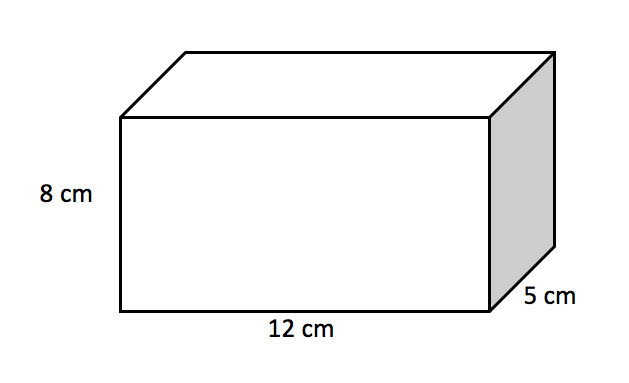
b) cube 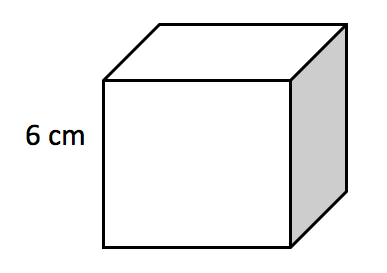
c) cylinder 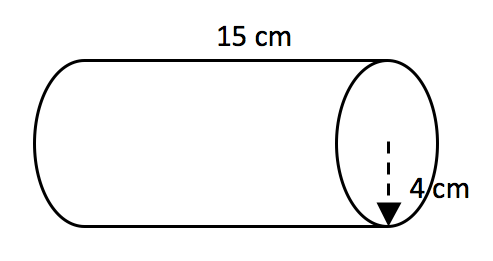
d) Triangular prism. Lengths are given to the nearest cm.
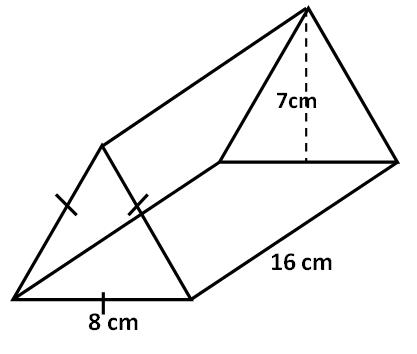
Click here to check your answers
The aim of this Big Idea was to develop the following understandings:
Measurement Big Idea 1 lists many of the standard units of measurement used daily in important areas of measurement such as length, mass, volume, time and temperature.
In this Big Idea you have revised the essential features of the concept of measurement. You have also revised the ideas of length, area and volume.
If you feel that you have a good understanding of these topic, please continue on with Big Idea 3 in the Measurement module.
Think of an athlete who regularly measures and compares personal attributes to check for maintenance or improvement of fitness. There may be certain indicators of personal fitness levels of which the athlete is aware, some of which are measurable and others which may be more difficult or impossible to measure accurately and objectively.
Which of the following properties do you think could be measured most accurately using a particular standard unit?
* Although the term weight is more commonly used, the correct term is mass. The two are different concepts. The mass of an object refers to how much matter is in the object, but the weight depends on how much gravity is acting on that mass. You may weight 59 kg on earth, but on the moon your weight would be much less!

Image source: Dog Foose
The athlete's mass would appear to be the most straightforward measure, assumed to be fairly accurate but limited by the calibration and precision of the scales. If weight was measured twice within a 5 minute time period, it is likely that the measure would be the same both times, especially if the unit measure of kilograms (kg) only goes to one decimal place e.g. , 72.3 kg.
However, there are factors other than scale collaboration which affect the accuracy of the measurement of the athlete's mass, such as the surface under the scales.
The accuracy of measurement of other factors such as heart rate, race time and race speed are influenced by an even wider range of variables such as personal health, sleep and outside temperature, but they can still be measured on a daily basis using units such as beats per minute and seconds to a number of decimal places using a stop watch.
Of the listed properties, sweat rate would probably be the most difficult to measure. There is no standard unit to measure this, so a method would have to be invented or devised, for example, measuring how much water is excreted through the skin. The level of accuracy would be difficult to measure and maintain.
Image source: NCTM Illuminations
Measurement is always approximate, in some cases less precise than others. Consideration must be given to variables such as the precision of the measuring device and even the person making the measurement.
Measurements made using small units, such as square millimetres, are more precise than measurements made using larger units, such as square centimetres.
Tiny, tiny measurements are called nano-measurements. For example, a nanometre is around 80 000 times smaller than the width of a human hair. Improved technology is allowing us to measure things that are very, very small.
Click on the following link from Annenberg Learner to learn how partitioning a measure into finer and finer sub-units increases precision and accuracy.
Consider the area of the figure with the red border below. The area within the red border/perimeter in the diagram below cannot be measured with much accuracy if only whole square units are used.
The number of whole square units shaded in pink within the border, is 48 square units. As these pink square units only touch the perimeter in a few places, leaving significant gaps, the measurement of 48 square units is obviously not enough to cover the area within the red border. If each square unit was a square paver or tile, 48 would not be enough to cover the area.
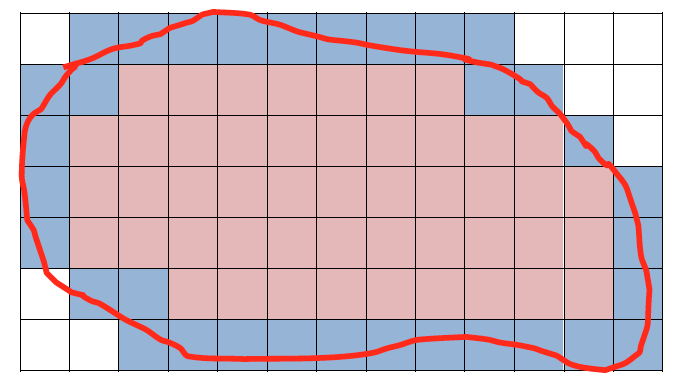
The 37 (blue) tiles protruding the perimeter would be needed as well, so the actual area of the tiles laid out on the floor would be 48 + 31, being square units.
When the tiles are cut to cover the area within the perimeter, so there are not gaps and no tiles protruding the perimeter, a more accurate measure of the tiled area could be made by subtracting the parts (fractions) of the blue tiles which go beyond the boundary. Estimate what you think the area within the red perimeter is, using this strategy.
Because the protruding (blue) parts add up to about 16 square units, your estimate should be close to 79 square units (79 – 16). The precision would not be great, as many the parts were probably estimated to be halves and quarters. If each tile was divided into one hundred square parts (10 x 10), then the fractions estimated could be approximated in hundredths rather than halves and quarters, increasing the level of precision.
Which of the two measurement devices in questions 1 to 3 gives a more accurate reading:
1. A stop watch to two decimal places or a stop watch to four decimal places?
2. A map with a scale of 1:100 or a scale of 1:10 000?
3. Kitchen scale A or B (below) to measure cooking ingredients.
A

Image source: Produto Direto
B

Image source: That Online Shop
4. The NailCo lab was collecting data on fingernail growth from participants trialling a new product. After twenty days the nail growth for most of the trial participants was recorded as 2 – 3 mm.
These measurements could have been much more precise, for example, if each mm was divided into tenths. The units of measurement could have been expressed in increments of tenths of millimetres or 0.1 mm. If one person's increase was recorded as 2.2mm and another's was 2.7mm, the significant difference of 0.5mm could be recognised. Measures of 2.56 mm or 2.07 mm for example would be even more precise, as each millimetre has been divided into hundredths.
The following measures fall between 2mm and 3mm. Identify which of these measures are the most precise, and which are the least precise:
a) 2.09 mm
b) 2.35 mm
c) 2.1 mm
d) 2.001 mm
e) 2.03 mm
f) 2. 8 mm
g) 2.365 mm
Click here to check your answers
For your interest…
The purpose of this Big Idea was to develop the following understandings:
Do you feel like you understand these now? If so continue on to Big Idea 4.
A map or plan represents a distance or area of much bigger size than the map itself, so measurements are scaled down to make the map of a size that can be conveniently used.
Shapes in a scaled down drawing have the same shape as the real thing. This could be the shape of a room on a house plan or the shape of the coastline on a map. Scaled drawings, such as those of builders and engineers, are used for construction of bridges and buildings.
A ratio (see FDRP module 2) can be used to represent scale.
Example 1:
A particular map scale might be 1:100 000. In this case, it means that 1cm on the map represents an actual distance 100 000 cm. Both quantities have the same unit of centimetres.
As 100 000cm = 1 000m = 1km, one centimetre on that map represents an actual distance of one kilometre. A length of 2cm on the map would therefore represent 2km, and 4cm would represent 4km.
Sometimes scales do not have the same unit for the two quantities that are being represented. For example the scale that has 1 cm representing 1 km might be written as 1cm:1km. This may be easier to interpret or visualise than the scale of 1cm:100 000cm.
The scale below shows 2cm on a map representing an actual distance of 2km.
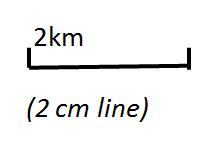
Learning Activity 1: Scale
Go to BBC UK's Bitesize Ratio
for scale drawing and map scale problems.
Click on 'reveal' to see explanations and to check your answers.
1. Express the scale 1cm to 10 000 m as a ratio where both quantities have the same unit.
2. Express the scale 5 mm to 100 m as a ratio where both quantities have the same unit.
3. Simplify the following scales:
a) 5cm to 2km = 1cm to _______m
b) 8 mm to 200m = ________mm to 100m
c) 1.5cm to 5km = ________cm to 10km
4. Use the scale diagram below to calculate the actual distance represented on the map:
a) 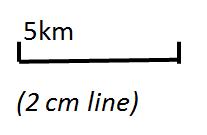
Distance on map is 6 cm
b)
Distance on map 10 cm
5. Explore Google maps on the Internet (do a search for google maps). Notice how as you enlarge the map, the actual distance stated on the scale at the bottom left hand corner gets smaller.
For example, a 2cm scale line may represent 50km, but as you enlarge the map by moving the slider up towards the ‘+’ symbol, the distance represented by the scale line decreases (this is written above the scale line in km, and below the scale line in miles).
Then as you decrease the size of the map by moving the slider down towards the
‘-’ symbol, the actual distance on the scale line increases as the map is smaller hence showing a greater area.
Click here to check your answers
When simplifying scale in the above practice activities, the relationships between the two numbers in the ratio needed to be retained.
Let's look at simplifying 5 cm to 2 km. Knowing that 2 km is 2000m and that there are 100 cm in a metre, we can work out that there are 2000 x 100 cm, or 200 000cm, in 2 km. The scale of 5 cm to 2 km can therefore also be expressed a ratio 5:200 000, as both numbers represent centimetres.
It is simpler to express the relationship between the two numbers as 1: x rather than 5: x (where x stands for a number) therefore the 5 cm is divided by 5 to change it to one. The 200 000 cm also needs to be five times smaller to maintain the relationship or proportions between the two distances, so the scale can be expressed as 1:40 000 or 1 cm to 0.4 km.
The relationship between the map distance and the actual distance has been retained each of the various scales of 5 cm to 2 km, 1 cm to 0.4 km, 5:200 000 and 1:40 000. To be able to use the concept of proportion to solve mathematical problems such as this shows the skill of proportional reasoning.
We often use proportional reasoning when measuring the *mass of ingredients when cooking.
* Although the term weight is more commonly used, the correct term is mass. The two are different concepts. The mass of an object refers to how much matter is in the object, but the weight depends on how much gravity is acting on that mass. You may weight 59 kg on earth, but on the moon your weight would be much less!
When using a recipe, the ingredients have relationships to each other. If a recipe requires 1 egg and 2 cups of flour, the relationship of eggs to cups of flour is 1 to 2. We can also say that the ratio of eggs to flour is 1:2.
Example 1:
The following ingredient list for a recipe makes 36 cookies:
Choc Chip Cookies* 
1 cup flour
1/2 tsp baking soda
1/2 tsp salt
1/2 cup butter
1/3 cup brown sugar
1/3 cup sugar
1 egg
1/2 tsp vanilla
1 cup chocolate chips
(makes 36)
Note: The "cup" measurement across the world is not the same. Have a look at Cup (unit) on Wikipedia for a discussion of the "cup".
Image source: 123RF
To make three lots of cookies so you have at least 100 cookies, it is important that the ratio between the ingredients, or the proportions, remain the same.
If one cup of flour is required for 36 cookies, then it is logical that 3 cups are required for 3 times as many cookies (108).
To maintain the proportions, the amount of every other ingredient will also need to be multiplied by 3, resulting in:
Choc Chip Cookies
3 cups flour
1 ½ tsp baking soda
1 ½ tsp salt
1 ½ cup butter
1 cup brown sugar
1 cup sugar
3 eggs
1 ½ tsp vanilla
3 cups chocolate chips
(makes 108)
|
|
|
Example 2:
The following ingredients for a recipe is for one serve of fruit punch.
To make a punch bowl of 24 serves we need to multiply the amount of each ingredient by 24.
Fruit Punch
One serve (250 ml) | 24 serves |
|---|---|
60 ml orange juice | 24 x 60 = 1440 ml |
40 ml mango juice | 24 x 40 = 960 ml |
40 ml pineapple juice | 24 x 40 = 960 ml |
10 ml fresh lemon juice | 24 x 10 = 240 ml |
100 ml soda water | 24 x 100 = 2400 |
See Measurement module 1 – Standard units of measure to help with conversions such as grams to kilograms.
1. The following ingredient list for a recipe makes 12 muffins. Rewrite the list to make 48 muffins.
Banana Apple Muffins
1 apple, about 125 gm
1/4 tsp cinnamon powder
2 medium - large ripe bananas, about 300 gm
60 gm melted butter
100 gm sugar
1 egg, beaten
125 ml milk
240 gm cake flour
1/4 tsp baking soda
1 tsp baking powder
1/8 tsp salt
2. The following ingredient list for recipe serves 8 people. Reduce the amount of each ingredient so the recipe makes only 4 serves.
Pumpkin and Sweet Potato Soup
1 kg pumpkin, peeled and diced
1 kg red sweet potatoes, peeled and diced
2 onions, diced
1 tsp minced ginger
1 tsp minced garlic
80 gm butter
2 tbsp vegetable oil
9 cups chicken stock
Salt and pepper to taste
Click here to check your answers
Measuring time and understanding and estimating duration of time are essential life skills. We always have to communicate with others about time.
The ability to understand how time is structured and measured is often vital in our everyday personal and professional lives. The structure of time measurement can be confusing when learning about time, as time is not always measured in base 10 (see Place Value module 1). This inconsistent structure of time measurement means that conversions between units of measure of time can be more complicated than other measurement conversions. The following diagram illustrates some time conversions:

Conversion examples:
| Convert 4 hours and 36 minutes to minutes | (4 x 60) + 36 = 276 minutes |
| Convert 2 hours, 14 minutes and 10 seconds to seconds | (2 x 60 x 60) + (14 x 60) + 10 = 8 050 seconds |
| Convert 948 minutes to hours | 948 ÷ 60 = 15 remainder 48 = 15.8 hours Explanation: The remaining 48 minutes is 48/60 parts of an hour i.e., 8/10 parts of an hour. |
| Convert 12 weeks into days | 12 x 7 = 84 days |
| Convert 5000 seconds to hours, minutes and seconds | 5000 ÷ 60 = 83 remainder 10 = 83 minutes and 10 seconds = 1 hour, 23 minutes and 10 seconds |
The following rhyme to help with remembering the number of days in each of the 12 months of the year has been used since the 15th century:

Another reason why the concept of time may be difficult to comprehend is that it cannot be seen or felt like other attributes that are commonly measured. Throughout history, different cultures have perceived time in different ways. For example, the Amondawa tribe has a different sense of time from western cultures.
Learning Activity 2: A brief history of time
Click on the link below from NRICH enriching mathematics to discover the development of time measurements and structures through history, such as why base 60 was adopted for seconds, hours, and minutes in relation to the movement of the sun.
Analogue clocks consist of a circular face divided by markings into 12 hours and usually into 60 minutes. They have two or three hands. The clock represented below has two hands.
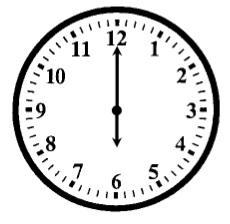
This short thick hand is used to measure the hours. One full revolution (360 degrees) of the hour hand on an analogue clock measures 12 hours of a day.
A longer and slightly thinner hand is used to measure minutes. The minute hand takes one hour to make a full revolution and each marking on the circle measures one minute. It takes five minutes to move from one number to the next.
Some clocks have a long thin hand to measure seconds. The second hand takes one minute or 60 seconds to make one full revolution with each marking on the circle measuring one second.
The clock below shows that in 25 seconds, the time will be approximately ten minutes past ten. This is written as 10:10 in digital time.

This clock shows the time as approximately 16 minutes and 12 seconds to one o'clock.
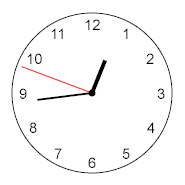
In digital time, 16 minutes to one o'clock is expressed as 12: 44. On the clock, the minute hand shows that 44 minutes have passed since 12 o'clock.
From the time you get out of bed you are probably estimating time:
You may not be aware of the skills and understandings you have developed to be able to estimate time.
To think of time as something that can be measured, it is helpful to compare two events that do not start at the same time.
You will also need to know about standard units to measure time, such as seconds, minutes and hours. This can be demonstrated in the following problem.
Sample thinking to solve the problem, "Will I have time to walk to the shop and back before my guests arrive?"

Image source: Clker.com
A comparison was made with a known measurement, that is, 8 minutes to walk to the school, which was estimated to be half the distance to the shop. Other variables were taken into consideration, such as speed of the travel (walking faster alone than with the kids) and time to buy one item. An understanding of clock reading was required, including minutes per hour.
A visual such as an empty number line can be used to demonstrate duration of time. The number lines below show the time it took to go to the shop and back, using the known measurement of the time it takes to walk to school as a benchmark to help with the time estimation.
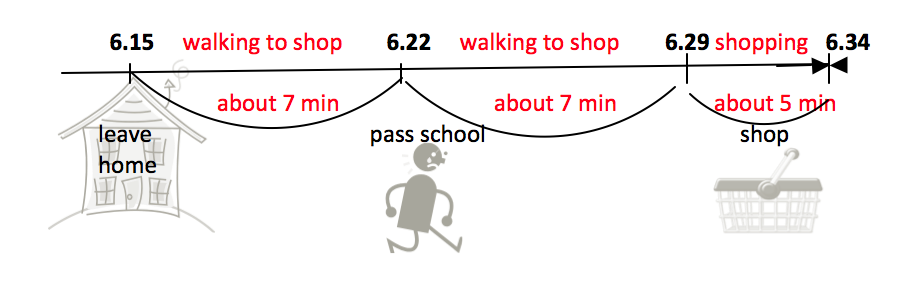
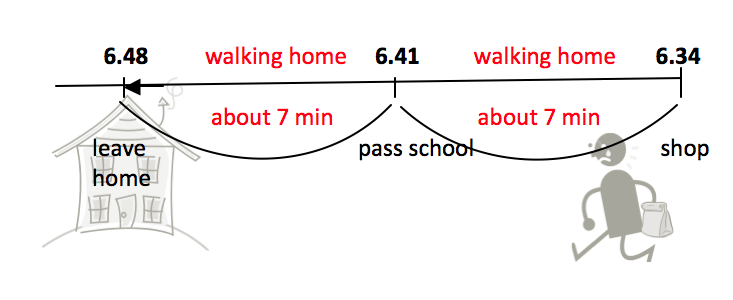
1. The floor plan below is of a new house. So far, bedrooms one and two have been painted. If it took four days to complete the painting of these two rooms, estimate in days how long it will take to paint the other three rooms. What is your reasoning?
Image source: Wikimedia Commons
2. Estimate how many minutes it would take to fold 48 towels. What is your reasoning?
3. Estimate how many shopping hours it would take to purchase all of the following for yourself in one shopping centre:
Explain your reasoning.
Click here to check your answers
Being able to read timetables is an important life skill, especially when having to get to class at the right place and time, catch transport or tune in to the right TV channel at the right time.
The Big Day Out timetable below shows the line up of artists at an all day concert event. It indicates where and what time each band or artist is performing.
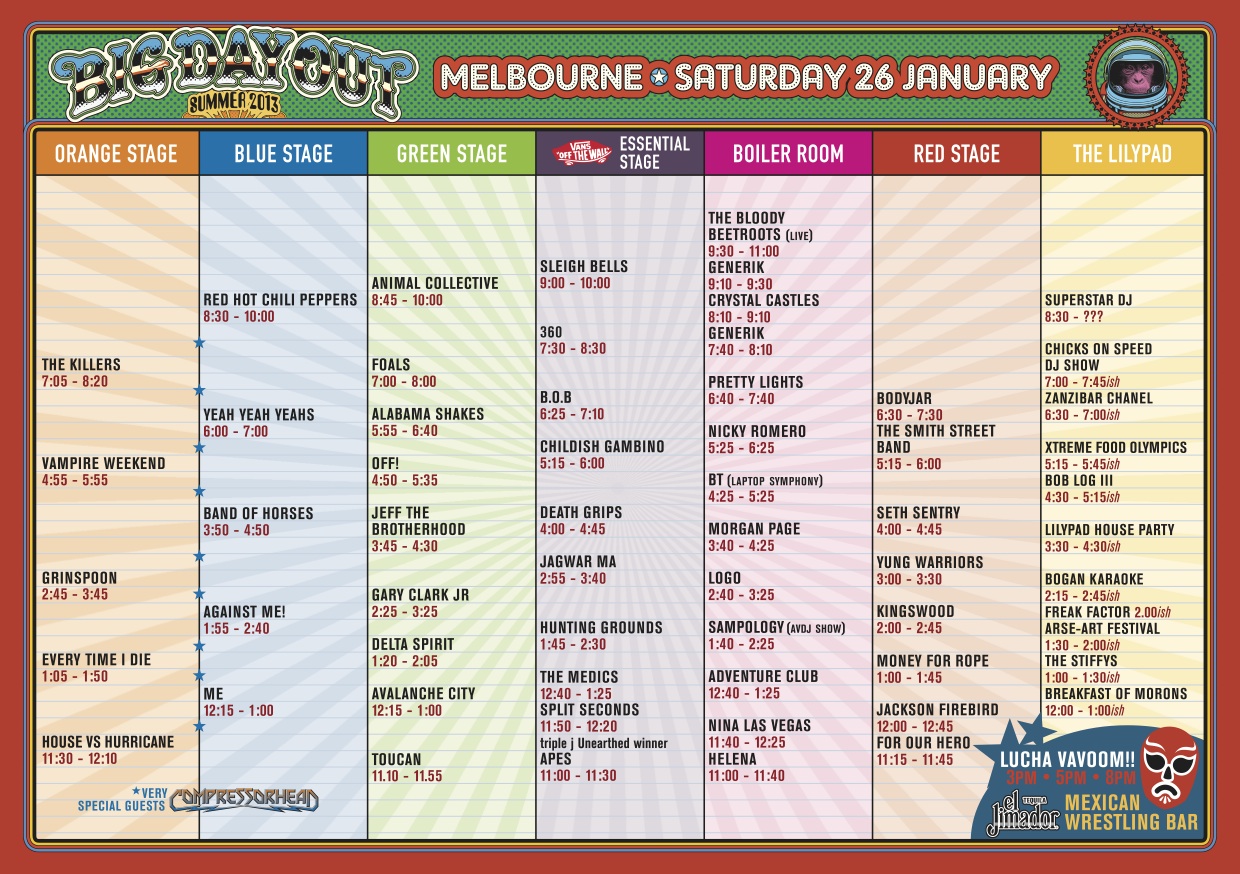
Here are some understandings and skills required to be able to follow the timetable:
Practice Task
Use the Big Day Out timetable above to answer the following questions:
Click here to check your answers
The aviation industry, the armed forces and hospitals use 24-hour time. Sometimes digital clocks display time in 24-hour time.
Twenty-four hour time means we start at 00:00 or 0000 at midnight and go through to 23:59 or 2359 ('twenty three fifty nine') just before midnight the next night. The first two digits measure the hours after midnight, and the second two digits measure the minutes. The colon is quite often not used.
The times before 1.00 pm are expressed in a similar way to the 12-hour clock for example 5.30 am in 12 hour time is expressed as 0530 ('oh five thirty') in 24-hour time, and 12.59 on a 12-hour clock is 1259 (twelve fifty nine) on a 24-hour clock.
The 12-hour times from 1 pm to 11.59 pm are expressed differently in 24-hour time. This is shown in the table below.
1:00 AM equals 01:00 ('oh one hundred') |
2:00 AM equals 02:00 ('oh two hundred') |
3:00 AM equals 03:00 ('oh three hundred') |
4:00 AM equals 04:00 ('oh four hundred') |
5:00 AM equals 05:00 ('oh five hundred') |
6:00 AM equals 06:00 ('oh six hundred') |
7:00 AM equals 07:00 ('oh seven hundred') |
8:00 AM equals 08:00 ('oh eight hundred') |
9:00 AM equals 09:00 ('oh nine hundred') |
10:00 AM equals 10:00 ('oh ten hundred') |
11:00 AM equals 11:00 ('oh eleven hundred') |
12:00 PM equals 12:00 ('twelve hundred') |
1:00 PM equals 13:00 ('thirteen hundred') |
2:00 PM equals 14:00 ('fourteen hundred') |
3:00 PM equals 15:00 ('fifteen hundred') |
4:00 PM equals 16:00 ('sixteen hundred') |
5:00 PM equals 17:00 ('seventeen hundred') |
6:00 PM equals 18:00 ('eighteen hundred') |
7:00 PM equals 19:00 ('nineteen hundred') |
8:00 PM equals 20:00 ('twenty hundred') |
9:00 PM equals 21:00 ('twenty one hundred') |
10:00 PM equals 22:00 ('twenty two hundred') |
11:00 PM equals 23:00 ('twenty three hundred') |
12:00 AM equals 00:00 ('twenty four hundred') |
Data source: L-Soft
Example:12-hour to 24-hour Time Conversion
1.00 pm in 24-hour time is 12 + 1 = 13:00 or 1300
5.00 pm in 24-hour time is 12 + 5 = 17:00 or 1700
8.30 pm in 24-hour time is 12 + 8 = 20:00 plus 30 minutes = 20:30 or 2030
10.45 pm in 24-hour time is 12 + 10 = 22:00 plus 45 minutes = 22:45 or 2245
Click on the following link to see more examples of converting am/pm time to 24-hour time. Complete the questions at the bottom of the page. Explanations are provided for incorrect answers.
The following London Sunday bus timetable uses 24-hour time to show what time the buses arrive at each station. For example:
Based on the timetable above answer the following questions:
Click here to check your answers
As the earth rotates, the part of the earth facing the sun experiences day time and the part facing away from the sun is experiencing night. If, for example, it is day time in Australia, it is night time in Europe.

The world is divided into time zones, as shown on the chart below. All places in a particular time zone (shown in vertical coloured regions under the clocks) have the same time, except for places that have turned the clock forward one hour during daylight savings time.
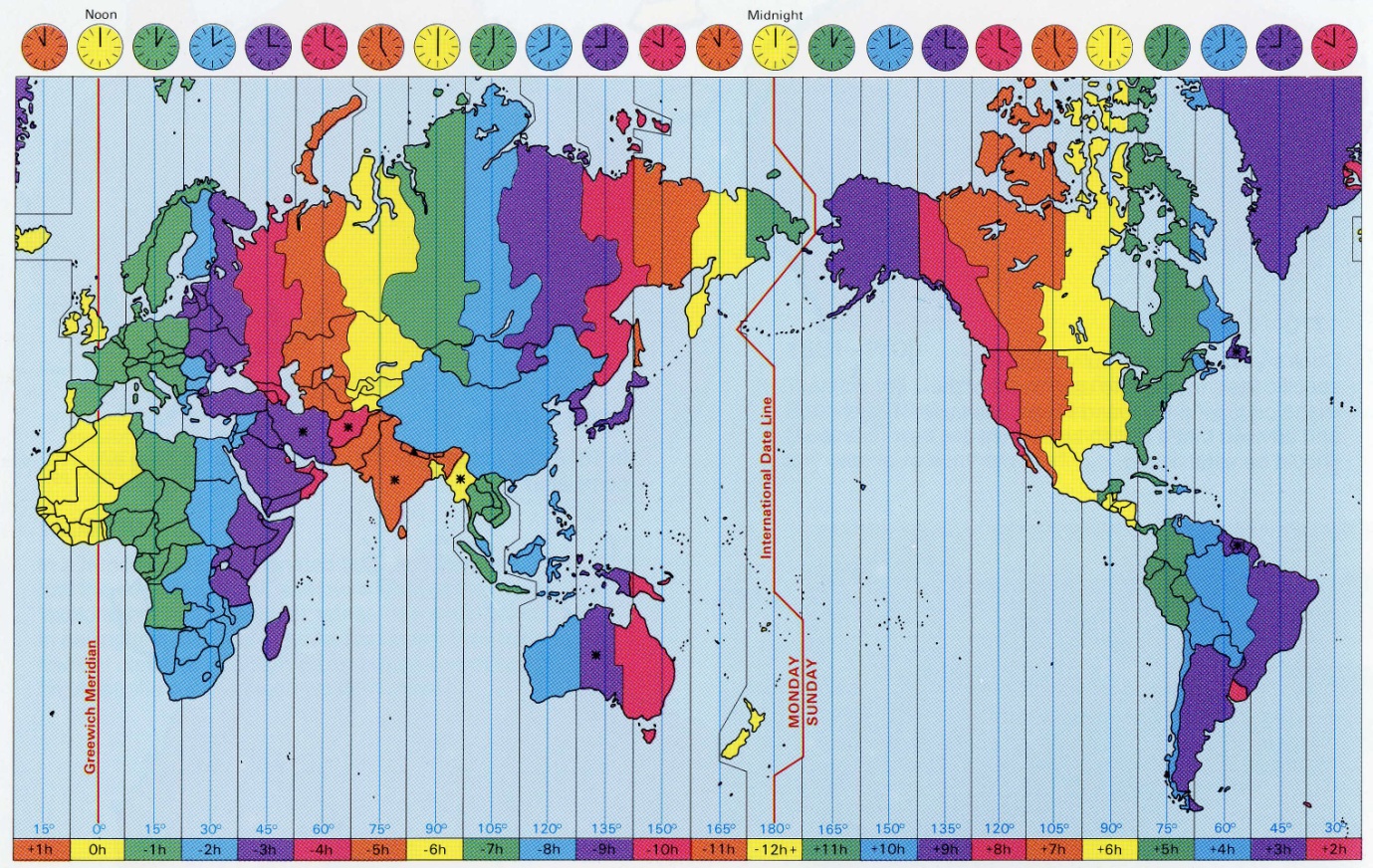
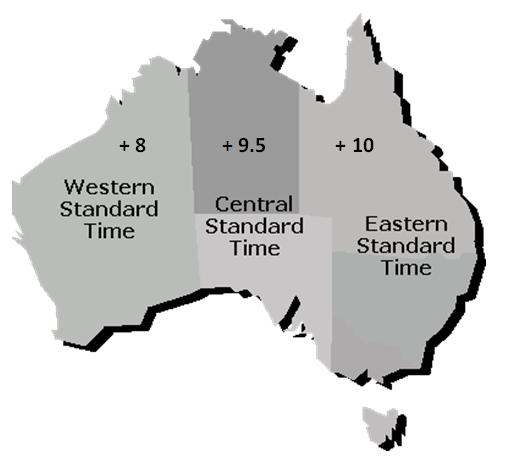
As Australia is a large country it has three different time zones, as shown below. The numbers on the map represent the hours ahead of Greenwich Meridian Time (GMT) in the London area, which is used as a world time reference.
Western Standard Time is 8 hours ahead of GMT, Central Standard Time is 9.5 hours ahead of GMT and Eastern Standard Time is 10 hours ahead of GMT. For example, if it is 7.00 am in Perth Western Australia, it will be 9.00 am in Sydney NSW or Melbourne Victoria (in non-daylight saving time) as the Eastern states' time zone is two hours ahead.
Learning Activity 4: Australian Time Zones Explained
Watch the following video, it will assist you to calculate times around Australia.
Click here to check your answers
The purpose of this module was to develop the following understandings:
Do you understand these concepts now? If so, you are ready to take the Measurement module quiz. Click here to access this quiz and then continue on to the next module.
Authorised by the Director, Centre for University Pathways and Partnership
2 May, 2018
Future Students | International Students | Postgraduate Students | Current Students
© University of Tasmania, Australia ABN 30 764 374 782 CRICOS Provider Code 00586B
Copyright | Privacy | Disclaimer | Web Accessibility | Site Feedback | Info line 13 8827 (13 UTAS)