Mathematician Madeleine Cockerill, a PhD student at the School of Natural Sciences, is studying what happens to bubbles if we let them be non-spherical.
“A standard assumption in maths is to assume that things are spherical because that makes everything easy,” explains Madeleine.
“But if you go out in the real world, not everything is spherical.
Typically, really small bubbles stay spherical because surface tension keeps them that way. But if you have larger bubbles, like from underwater explosions, the bubbles get non-spherical.
However, Madeleine isn’t out in the field measuring bubbles with a measuring tape, her study is theoretical, using models to understand the process.
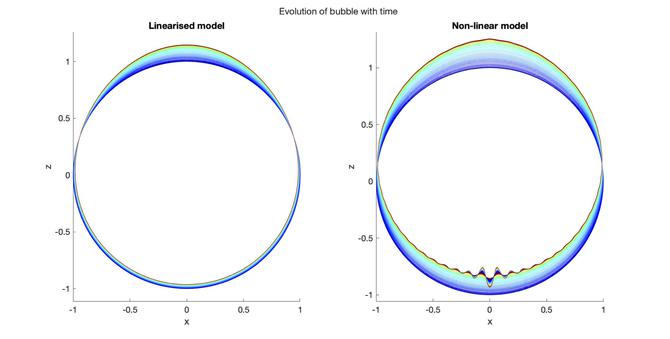
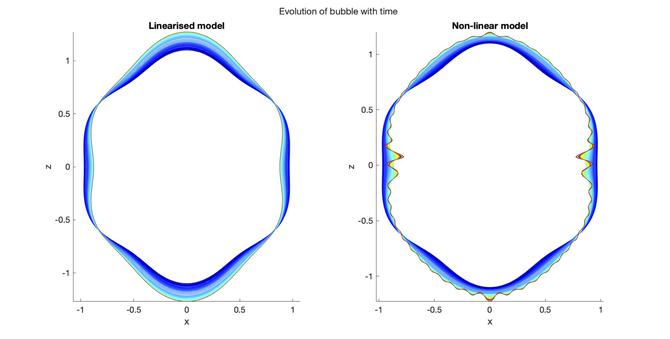
“First of all, we're looking at a linear model, which is where we start by saying that we have a spherical bubble and make a tiny disturbance to observe what happens. However, if the disturbance is big, the model no longer works,” explains Madeleine.
“We've also got a non-linear model, which works with bigger disturbances and is a combination of analytic and numerical techniques.
“When we started, we didn't account for things like gravity, surface tension or viscosity. But as we keep going, we add more and more of these elements, making the model more complex and more realistic.”
Developing an understanding of the ability of bubbles to be non-spherical is important for a wide range of different fields.
Madeleine’s work can be applied to marine work, such as understanding underwater explosions which can involve dome or doughnut-shaped bubbles. It also expands our knowledge on cavitation bubbles and sonoluminescence, which are important for developing propellers for ships and ultrasonics.
“It has applications in astrophysics where you have "space bubbles", which are massive non-spherical bubbles that often develop jets - this work could allow us to further understand these phenomena,” says Madeleine.

The work could also have a range of engineering applications, such as the cooling of nuclear reactors.
Only six months into her PhD, Madeleine has already published one paper from her honours work, with another manuscript currently in the proofing stage.
“We were looking at topographic waves in the polar basin, which are very long, very slow waves that take months to travel across oceans. You need satellites to see them, but they're caused by the rotation of the Earth and the changes of depth in the ocean basin,” explained Madeleine.
“My supervisors had been modelling these waves, assuming that the basin is one constant depth, then they tried with the addition of a constant step-shelf. However, the real basin has a curved shelf, so we wondered how do we make this more realistic? And that's where my paper came in, applying that curve to the models.”
Madeleine’s love for maths began at a young age where she “always thought the coolest thing would be to be a maths professor.”
“In high school, when we had to write about celebrities we looked up to, I wrote about mathematicians Andrew Wiles and Blaise Pascal,” says Madeleine. “Since then, I’ve just kept doing more and more maths.”
As the recipient of the 2020 Edith Rita Lowenstern Prize for greatest proficiency and achievement with first-class Honours in Mathematics, Madeleine is well on her way to fulfilling that professorship dream.